If g=GM/r2, then where will the value of g be high, at Goa Beach or on the top of the Mount Everest ?
Video Solution
Text Solution
The value of g will be high at Goa Beach.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GRAVITATION EXERCISE - Give scientific reasons :3videos
GRAVITATION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GRAVITATION EXERCISE - Distinguish between :2videos
GRAVITATION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GRAVITATION EXERCISE - QUESTIONS & ANSWERS45videos
GRAVITATION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GIVE SCIENTIFIC REASONS EXERCISE - CHAPTER 10 : DISASTER MANAGEMENT2videos
GIVE SCIENTIFIC REASONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - HEATEXERCISE - NUMERICAL PROBLEMS FOR PRACTICE12videos
HEAT
Similar Questions
Knowledge Check
- Question 1 - Select One
A man can jump 2 m high on the surface of the earth. How high he can jump on a planet where the acceleration due to gravity is g12, where g is the acceleration due to gravity on the surface of the earth ?
A12 mB18 mC24 mD30 m - Question 2 - Select One
Calculate the mass in gm of 2g atom of Mg-
A12 gmB24 gmC6 gmD48 gm - Question 3 - Select One
If G1,G2 are the geometric means fo two series of observations and G is the GM of the ratios of the corresponding observations then G is equal to
AG1G2BlogG1−logG2ClogG1logG2Dlog(G1⋅G2)
Where will the value of acceleration due to gravity (g) be less, at gateway of india or at the top of mount everest ?
View SolutionThe acceleration due to gravity at a height h is given by gh=g(RR+h)2, where g is the accleeration due to gravity on the surface of earth. For h<<R, find the value of g using the Binomial theorem.
View SolutionWhat are the factors affecting the value of g. Where is the value of g maximum ?
View SolutionWhat is the acceleration due to gravity on the top of Mount Everest? Mount Everest is the highest mountain peak o het workd at the height of 8848 m. The value at see level is 9.80ms−2.
View SolutionFind the G.M. of 4 and 9.
View Solution


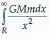 , where G,M and m are constants.
, where G,M and m are constants.