Two identical charged spherical drops each of capacitance C merge to from a single drop. The resultant capacitance is
equal to 2C
greater than 2C
less than 2c but greater than C
less than C
The correct Answer is:C
To find the resultant capacitance when two identical charged spherical drops, each with capacitance C, merge to form a single drop, we can follow these steps:
Step 1: Understand the Concept of Capacitance
The capacitance C of a spherical conductor is given by the formula:
C=4πϵ0r
where r is the radius of the sphere and ϵ0 is the permittivity of free space.
Step 2: Calculate the Volume of the Drops
The volume V of a single spherical drop is given by:
V=43πr3
For two identical drops, the total volume Vtotal is:
Vtotal=2×43πr3=83πr3
Step 3: Find the Radius of the Merged Drop
Let the radius of the new larger drop be R. The volume of the larger drop can be expressed as:
Vnew=43πR3
Since the total volume is conserved, we equate the two volumes:
83πr3=43πR3
By simplifying, we can cancel 43π from both sides:
2r3=R3
Taking the cube root of both sides gives:
R=21/3r
Step 4: Calculate the Capacitance of the New Drop
Now, we can find the capacitance Cnew of the new drop using the formula for capacitance:
Cnew=4πϵ0R
Substituting R=21/3r:
Cnew=4πϵ0(21/3r)
Since C=4πϵ0r, we can express Cnew in terms of C:
Cnew=21/3×C
Step 5: Conclusion
Thus, the resultant capacitance when two identical charged spherical drops merge is:
Cnew=21/3C
The capacitance C of a spherical conductor is given by the formula:
C=4πϵ0r
where r is the radius of the sphere and ϵ0 is the permittivity of free space.
The volume V of a single spherical drop is given by:
V=43πr3
For two identical drops, the total volume Vtotal is:
Vtotal=2×43πr3=83πr3
Let the radius of the new larger drop be R. The volume of the larger drop can be expressed as:
Vnew=43πR3
Since the total volume is conserved, we equate the two volumes:
83πr3=43πR3
By simplifying, we can cancel 43π from both sides:
2r3=R3
Taking the cube root of both sides gives:
R=21/3r
Now, we can find the capacitance Cnew of the new drop using the formula for capacitance:
Cnew=4πϵ0R
Substituting R=21/3r:
Cnew=4πϵ0(21/3r)
Since C=4πϵ0r, we can express Cnew in terms of C:
Cnew=21/3×C
Thus, the resultant capacitance when two identical charged spherical drops merge is:
Cnew=21/3C
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Grouping Of Capacitors48videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor Circuits52videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor32videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Twelve identical capacitors of capacitance C are connected across each edge of a cube. Find equivalent capacitance across one of the edges.
View SolutionSixty four identical sphere of change q and capacitance C each are combined to form a large sphere . The charge and capacitance of the large sphere is
View Solution
Knowledge Check
- Question 1 - Select One
Three condensers each of capacitance 2F are put in series. The resultant capacitance is
A6FB32FC23FD5F - Question 2 - Select One or More
There are 10 identical capacitors each of capacitance C.
AIf all of them are connected in series, their equivalent capacitance is C/10BIf all of them are connected in parallel, their equivalent capacitance is 10CCIf two series combinations each having 5 capacitors are connected in parallel, their equivalent capacitance is 2C/5DIf they are connected as five parallel combinations each one having two capacitors in series, their equivalent capacitance is 5C/2. - Question 3 - Select One
Two drops of a liquid are merged to form a single drop . In this process,
Aenetgy is releasedBenergy is absorbedCenergy remains constant .Dfirst (B) then (C )
A network of six identical capacitors, each of capacitance C is formed as shown below. The equivalent capacitance between the point A and B is
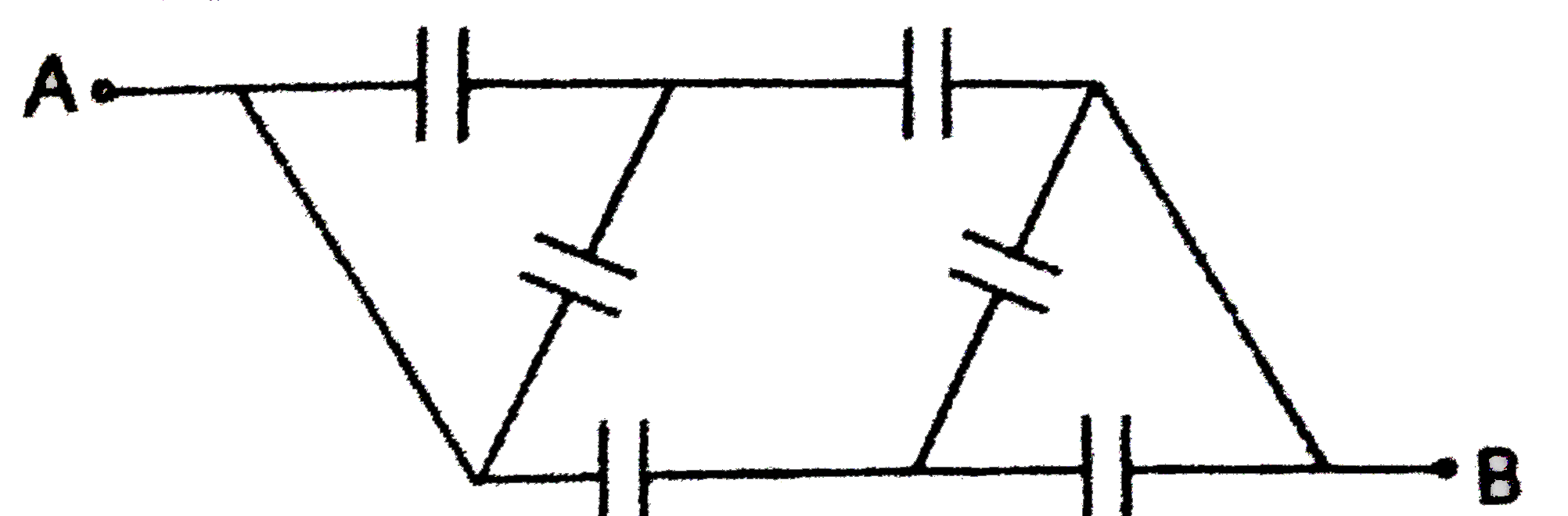 View Solution
View Solution1000 small water drops each of capacitance C join together to form one large spherical drop. The capacitance of bigger sphere is
View SolutionTwo condensers each of 4μF capacitance are joined in parallel. The resultant capacitance of the combination is
View SolutionSixty four spherical drops each of radius 2cm and carrying 5C charge combine to form a bigger drop. Its capacity is.
View SolutionTwo identical capacitors each of capacitance C are charged to the same potential V and are connected in two circuits (i) and (ii) at t=0 as shown. The charged on the capacitor at t=CR are
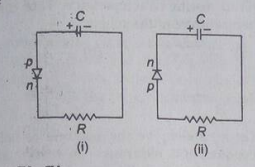 View Solution
View Solution

