Three concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−σandσ respectively. If VA,VB and VC denote the potentials of the three shells, then for c=a+b, we have
VC=VA≠VB
VC=VB≠VA
VC≠VB≠VA
VC=VB=VA
The correct Answer is:A
To solve the problem of finding the potentials VA, VB, and VC for three concentric spherical shells with given surface charge densities and radii, we can follow these steps:
Step 1: Understand the Configuration
We have three concentric spherical shells:
- Inner shell (radius a, surface charge density σ)
- Middle shell (radius b, surface charge density −σ)
- Outer shell (radius c, surface charge density σ)
Given that c=a+b.
Step 2: Calculate the Potential VA
The potential VA at the surface of the inner shell is due to the charge on all three shells:
VA=k(Q1a+Q2a+Q3a)
Where:
- Q1=σ⋅4πa2 (charge on the inner shell)
- Q2=−σ⋅4πb2 (charge on the middle shell)
- Q3=σ⋅4πc2 (charge on the outer shell)
Substituting these values:
VA=k(σ⋅4πa2a−σ⋅4πb2a+σ⋅4πc2a)
=k⋅4πσ(a−b2a+c2a)
Step 3: Calculate the Potential VB
For the middle shell, the potential VB is influenced by the inner and outer shells:
VB=k(Q1b+Q2b+Q3b)
Substituting the charges:
VB=k(σ⋅4πa2b−σ⋅4πb2b+σ⋅4πc2b)
=k⋅4πσ(a2b−b+c2b)
Step 4: Calculate the Potential VC
For the outer shell, the potential VC is:
VC=k(Q1c+Q2c+Q3c)
Substituting the charges:
VC=k(σ⋅4πa2c−σ⋅4πb2c+σ⋅4πc2c)
=k⋅4πσ(a2c−b2c+c)
Step 5: Simplify and Compare Potentials
Now, we need to simplify VA, VB, and VC and compare them. Since c=a+b, we can substitute this into our equations and simplify.
After simplification, we find that:
VA=VC
and
VB≠VA
Conclusion
Thus, we conclude that:
VC=VAandVB≠VA
We have three concentric spherical shells:
- Inner shell (radius a, surface charge density σ)
- Middle shell (radius b, surface charge density −σ)
- Outer shell (radius c, surface charge density σ)
Given that c=a+b.
The potential VA at the surface of the inner shell is due to the charge on all three shells:
VA=k(Q1a+Q2a+Q3a)
Where:
- Q1=σ⋅4πa2 (charge on the inner shell)
- Q2=−σ⋅4πb2 (charge on the middle shell)
- Q3=σ⋅4πc2 (charge on the outer shell)
VA=k(σ⋅4πa2a−σ⋅4πb2a+σ⋅4πc2a)
=k⋅4πσ(a−b2a+c2a)
For the middle shell, the potential VB is influenced by the inner and outer shells:
VB=k(Q1b+Q2b+Q3b)
Substituting the charges:
VB=k(σ⋅4πa2b−σ⋅4πb2b+σ⋅4πc2b)
=k⋅4πσ(a2b−b+c2b)
For the outer shell, the potential VC is:
VC=k(Q1c+Q2c+Q3c)
Substituting the charges:
VC=k(σ⋅4πa2c−σ⋅4πb2c+σ⋅4πc2c)
=k⋅4πσ(a2c−b2c+c)
Now, we need to simplify VA, VB, and VC and compare them. Since c=a+b, we can substitute this into our equations and simplify.
VA=VC
and
VB≠VA
Thus, we conclude that:
VC=VAandVB≠VA
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - AIIMS Questions20videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Assertion Reason8videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section B - Assertion Reasoning17videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Three concentric spherical metallic shells A,B,andC of radii a,b,andc(a<b<c) have surface charge densities σ,−σ and σ, respectively.
If VA,VB and VC are potential of shells A, B and C, respectively, match the columns
Column AColumn Ba.VAi.σε0[a2−b2+c2c]b.VBii.σ2ε0[a2b−b+c]c.VCiii.σε0[a−b+c]View SolutionThree concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.View Solution
Knowledge Check
- Question 1 - Select One
Three concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−σ and σ respectively. If VA,vB and Vc denote the potentials of the three shells, then, for VA=VC, we get-
Ac=a+b2Bc=b−aCc=2(a+b)Dc=a+b - Question 2 - Select One
Three concentric spherical metallic spheres A,B and C of radii a,b and c(a<b<c) have surface charge densities σ,−σ and σ respectively.
AThe potential of shell A:
VA=σε0(a+b+c)BThe potential of shell B:
VB=σε0(a2b−b+c)CThe potential of shell C:
VC=σε0(a2−b2c+c)DAll options are correct - Question 3 - Select One
Three concentric metallic spherical shells A,B and C of radii a,band c(a<b<c) have surface charge densities −σ,+σand -sigma respectively,thepotentialofshellA is
A(σ/ε0)[a+b−c]B(σ/ε0)[a−b+c]C(σ/ε0)[b−a−c]Dnone
Three concentric metallic shells A, B and C of radii a, b and c(a<b<c) have surface charge densities +σ,−σand+σ respectively as shown. Obtain the expressions for the potential of three shells A, B and C. If shells A and C are at the same potential, obtain the relation between a, b and c.
 View Solution
View SolutionThree concentric metallic shells A , B and C of radii a, b and c (a<b<c) have surface densities +σ,−σ and +σ respectively as shown in Fig.
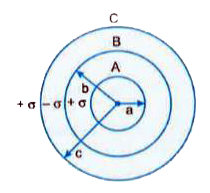
Obtain the expressions for the potential of three shells A , B and C .View SolutionThree concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.View SolutionThree concentric spherical metallic shells A,B and C of radii a,b and c (a<b<c) have surface charge densities σ,−σandσ respectively.
If the potenital of sheel B is VB=σ∈0(anb−b+c) and the potential of shell C is VC=σ∈0(anc−bnc+c) then n is .View SolutionThree concentric metallic spherical shell A,B and C or radiin a,b and C (a<b>C) have surface charge densities −singama,+σ, and −aigba respectively .
The potential of shell A is :View Solution

