Current flows through a metallic conductor whose area of cross-section increases in the direction of the current. If we move in this direction.
the current will change
the carrier density will change
the drift velocity will increase
the drift velocity will decrease
The correct Answer is:D
To solve the problem, we need to analyze the situation where current flows through a metallic conductor with an increasing area of cross-section in the direction of the current. We will look into how this affects the current, carrier density, and drift velocity.
1. Understanding the Current:
- The current I in a conductor is defined by the equation:
I=n⋅A⋅e⋅vd
where:
- n = carrier density (number of charge carriers per unit volume)
- A = cross-sectional area of the conductor
- e = charge of the carrier (for electrons, e≈1.6×10−19 C)
- vd = drift velocity of the charge carriers.
2. Current Flowing Through the Conductor:
- Since the current is flowing through the conductor, we need to consider whether the current I changes as we move along the conductor. In a steady state, the current remains constant throughout the conductor, regardless of changes in the area of cross-section. Therefore, we conclude:
I=constant
3. Carrier Density:
- The carrier density n is defined as the number of charge carriers per unit volume. In a metallic conductor, this value is typically constant for a given material and does not change with the area of cross-section. Thus, we conclude:
n=constant
4. Drift Velocity:
- From the equation I=n⋅A⋅e⋅vd, we can rearrange it to find the drift velocity:
vd=In⋅A⋅e
- Since I and n are constant, and e (the charge of the electron) is also constant, we can see that drift velocity vd is inversely proportional to the cross-sectional area A:
vd∝1A
- As we move in the direction of the current, the area A increases. Therefore, as A increases, vd must decrease:
vd decreases
Conclusion:
- Current: Remains constant.
- Carrier Density: Remains constant.
- Drift Velocity: Decreases as the area of cross-section increases.
- The current I in a conductor is defined by the equation:
I=n⋅A⋅e⋅vd
where:
- n = carrier density (number of charge carriers per unit volume)
- A = cross-sectional area of the conductor
- e = charge of the carrier (for electrons, e≈1.6×10−19 C)
- vd = drift velocity of the charge carriers.
- Since the current is flowing through the conductor, we need to consider whether the current I changes as we move along the conductor. In a steady state, the current remains constant throughout the conductor, regardless of changes in the area of cross-section. Therefore, we conclude:
I=constant
- The carrier density n is defined as the number of charge carriers per unit volume. In a metallic conductor, this value is typically constant for a given material and does not change with the area of cross-section. Thus, we conclude:
n=constant
- From the equation I=n⋅A⋅e⋅vd, we can rearrange it to find the drift velocity:
vd=In⋅A⋅e
- Since I and n are constant, and e (the charge of the electron) is also constant, we can see that drift velocity vd is inversely proportional to the cross-sectional area A:
vd∝1A
- As we move in the direction of the current, the area A increases. Therefore, as A increases, vd must decrease:
vd decreases
- Current: Remains constant.
- Carrier Density: Remains constant.
- Drift Velocity: Decreases as the area of cross-section increases.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Combination And Resistivity38videos
CURRENT ELECTRICITY
- BOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Kircoff'S Laws And Simple Circuits64videos
CURRENT ELECTRICITY
- BOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test30videos
ATOMIC PHYSICS
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test30videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
When a steady current flows through a metal conductor of non-uniform cross-section , then drift velocity is
AIndependent of area of cross-sectionBDirectly proportional to the area of cross-sectionCInversely proportional to the area of cross-sectionDInversely proportional to the square of area of cross-section. - Question 2 - Select One or More
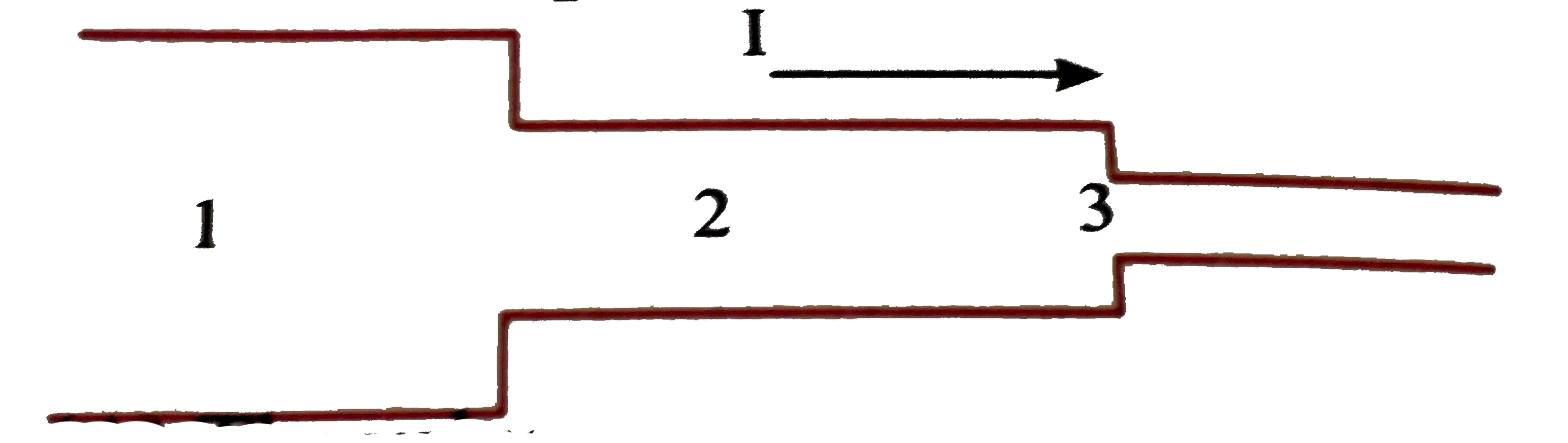
A steady current flows through the conductor of variable cross-sectional area. Now select the correct options.AThe value of current is same through the cross sections 1,2, and 3BThe current density is the maximum at the cross sections 3CThe drift velocity is greater at the cross-section 1DThe electric field is maximum at the cross section 3. - Question 3 - Select One
A steady current I is set up in a wire whose cross-sectional area decreases in the direction of the flow of the current. Then, as we examine the narrowing region
Athe current density decreases in value.Bthe magnitude of the electric field increases.Cthe current density remains constant.Dthe average speed of the moving charges remains constant.
What is the direction of electric current in a metallic conductors?
View SolutionA steady current flows in a metallic conductor of non-uniform cross-section. The quantity/ quantities constant along the length of the conductor is/are
View SolutionA steady current flows in a metallic conductor of non-uniform cross-section i.e., i : constant. A≠ constant.
View SolutionIf one ampere current flows through a conductor, the number of electrons flowing across the cross section of the conductor in 2 second it _________.
View SolutionA stready current i is flowing through a conductor of uniform cross-section. Any segment of the conductor has
View Solution


