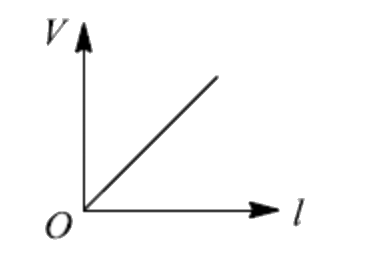
I−V characteristics of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
More if the experiment is performed at higher temperature
More if a wire of steel of same dimension is used
More if the length of the wire increased
Less if the length of the wire is increased
The correct Answer is:D
(d) Slope of V−i curve =R(=ρlA). But in given curve axis of i and V are interchanged. So slope of given curve
=1R(=Aρl) i.e., with the increase in length of the wire. Slope of the curve will decrease.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Combination And Resistivity
38 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Kircoff'S Laws And Simple Circuits
64 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
I−V characteristics of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
 AMore if the experiment is performed at higher temperatureBMore if a wire of steel of same dimension is usedCMore if the length of the wire increasedDLess if the length of the wire is increased
AMore if the experiment is performed at higher temperatureBMore if a wire of steel of same dimension is usedCMore if the length of the wire increasedDLess if the length of the wire is increasedl-V characteristic of a copper wire of length Land area of cross-section A is shown in figure. The slope of the curve becomes
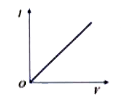 AMore if the experiment is performed at higher temperatureBMore if a wire of steel of same dimension is usedCMore if the length of the wire is increasedDLess if the length of the wire is increased
AMore if the experiment is performed at higher temperatureBMore if a wire of steel of same dimension is usedCMore if the length of the wire is increasedDLess if the length of the wire is increasedThe current -voltage - variation for a wire of copper of length (L) and area (A) is shown in fig. The slope of the line will be
 Aless if experiment is done at a heigher temperatureBmore if a wire of silver of same dimension is usedCwill be doubled if the lengths of the wire is doubledDwill be halved if the length is doubled
Aless if experiment is done at a heigher temperatureBmore if a wire of silver of same dimension is usedCwill be doubled if the lengths of the wire is doubledDwill be halved if the length is doubled
When length of a metal wire is doubled and area of cross-section is reduced to half, then its resistance becomes
View SolutionA metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod is
View SolutionIf breaking stress of a wire of length L and radius of cross-section r is P N/m2, then breaking stress of wire of same material of length 2 L and radius of cross section (r/2) will be
View SolutionThe resistance of wire of length l and area of cross-section a is x ohm. If the wire is stretched to double its length, its resistance would become:
View Solution