A constant current I is flowing through a circular coil placed in uniform magnetic field →B as shown. Then:

The loop is in stable equilibrium
The loop is in unstable equilibrium
The torque acting on the loop is maximum
The torque acting on the loop is 1√2 times the maximum torque
The correct Answer is:C
Torque acting on the loop is τ=M×B=Mbsinθ
Where θ= angle between M and B
In the figure shown θ=90∘ because B is in place of loop.
Or τ=MB=maximum torque
Hence, (c) is correct and choice (d) is wrong.
Since, torque is acting on the loop so loop is not in equilibrium.
Hence, choices (a) and (b) are wrong.
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Current
44 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Circular Arc
69 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Force On A Current Carrying Conductor In Magnetic Field
42 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Knowledge Check
A wire of length l is bent in the form a circular coil of some turns. A current I flows through the coil. The coil is placed in a uniform magnetic field B. The maximum torqur on the coil can be
AiBl24πBiBl2πCiBl22πD2iBl2πCurrent I is flowing through a circular coil of radius r. It is placed in a magnetic field B0 in such a way that the plane of the circular coil is perpendicular to B0. The force acting in it will be -
AπIrB0BIrB0CzeroD2πIrB0A current passing through a circular coil of two turns produces a magnetic field B as its centr. The coil is then rewound so as to have four turns and the same current is passed through it. The magnetic field at its centre now is
A2BBB/2CB/4D4B
A coil carrying electric current is placed in uniform magnetic field, then
View SolutionThe (τ−θ) graph for a current carrying coil placed in a uniform magnetic field is
View SolutionAs current I flowing through the loop as shown in figure. The magnetic field at the centre O is
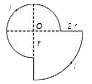
View SolutionA current i flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
View SolutionA current i flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
View Solution
