A square loop ABCD of side 'a' carrying current I is folded about an axis passing through its centre (y-axis). The two halves are inclined at angle 30∘ with xy plane as shown. Find the magnetic field at origin. The origin coincides with the centre of loop.

μ0I√3√2πa
μ0I√32√2πa
3μ0I2√2πa
√6μ0Iπa
The correct Answer is:D
Bnet=2(Bhalf)cosθ
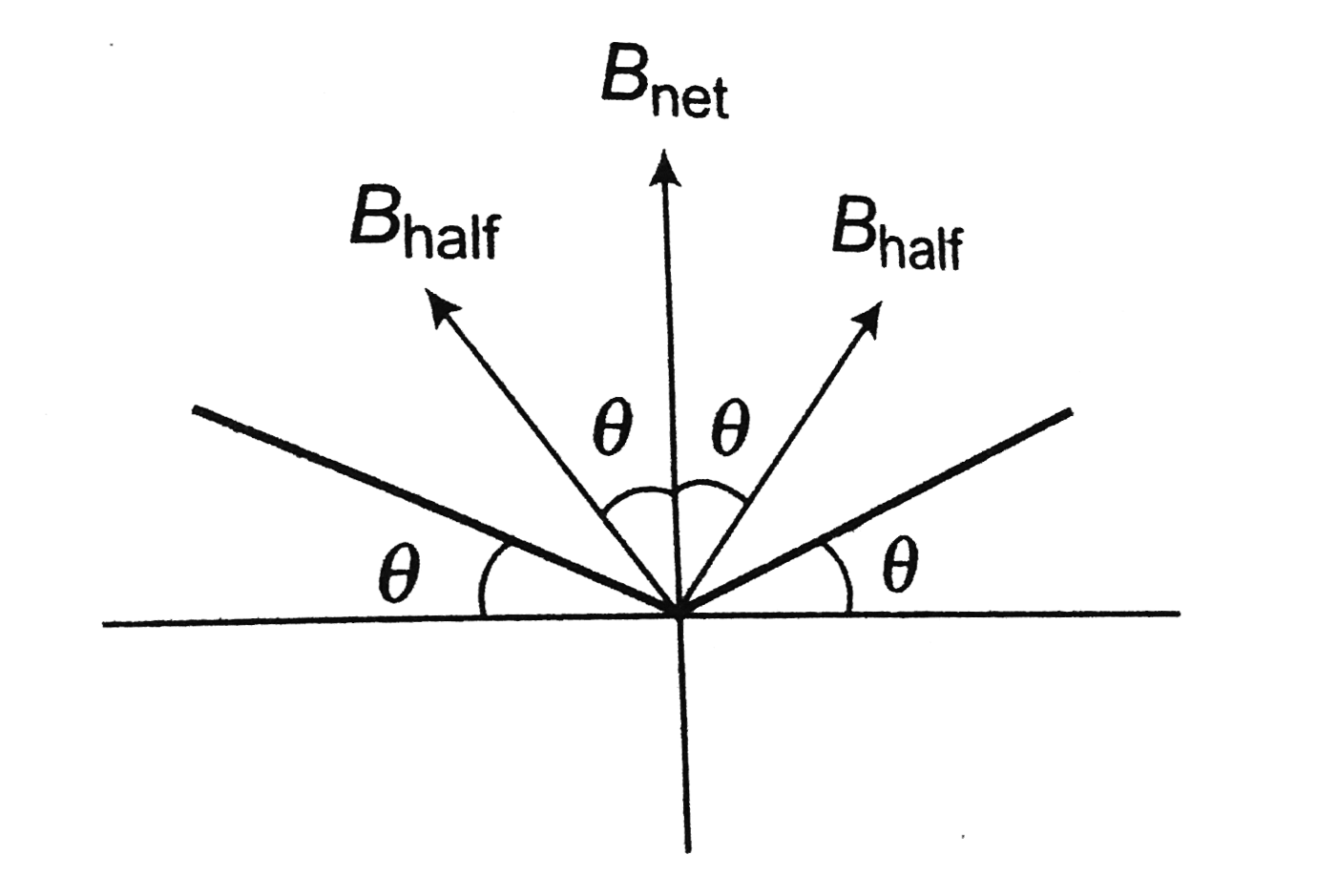
Where Bhalf=12[4μ04πI(a/2)](cos45∘+cos45∘)
=μ0I√2πa
So, B=2(μ0I√2πa)√32=√6μ0Iπa
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning
31 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - AIPMTNEET Questions
47 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Circular Arc
69 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Knowledge Check
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
Aμ0l2√2πaB2√2μ0lπaCμ0l√2πaDμ0l√2πaA square loop of side l carrying current I is part of the shown arrangement . Minium current I to just move the block up the inclined plane is
 Amgsinθ+μmgcosθBlBmgsinθ+μmgcosθ2BlC2mgsinθ+2μmgcosθBlDmgsinθ−μmgcosθBl
Amgsinθ+μmgcosθBlBmgsinθ+μmgcosθ2BlC2mgsinθ+2μmgcosθBlDmgsinθ−μmgcosθBl
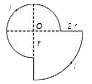
As current I flowing through the loop as shown in figure. The magnetic field at the centre O is
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionA circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
View SolutionA current I flows through a closed loop as shown in figure. The magnetic field induction at the centre 0 is

View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View Solution

