A long straight wire of radius a carries a steady current I. The current is uniformly distributed over its cross-section. The ratio of the magnetic fields B and B' , at radial distances a2 and 2a respectively from the axis of the wire is:
14
12
1
4
The correct Answer is:C
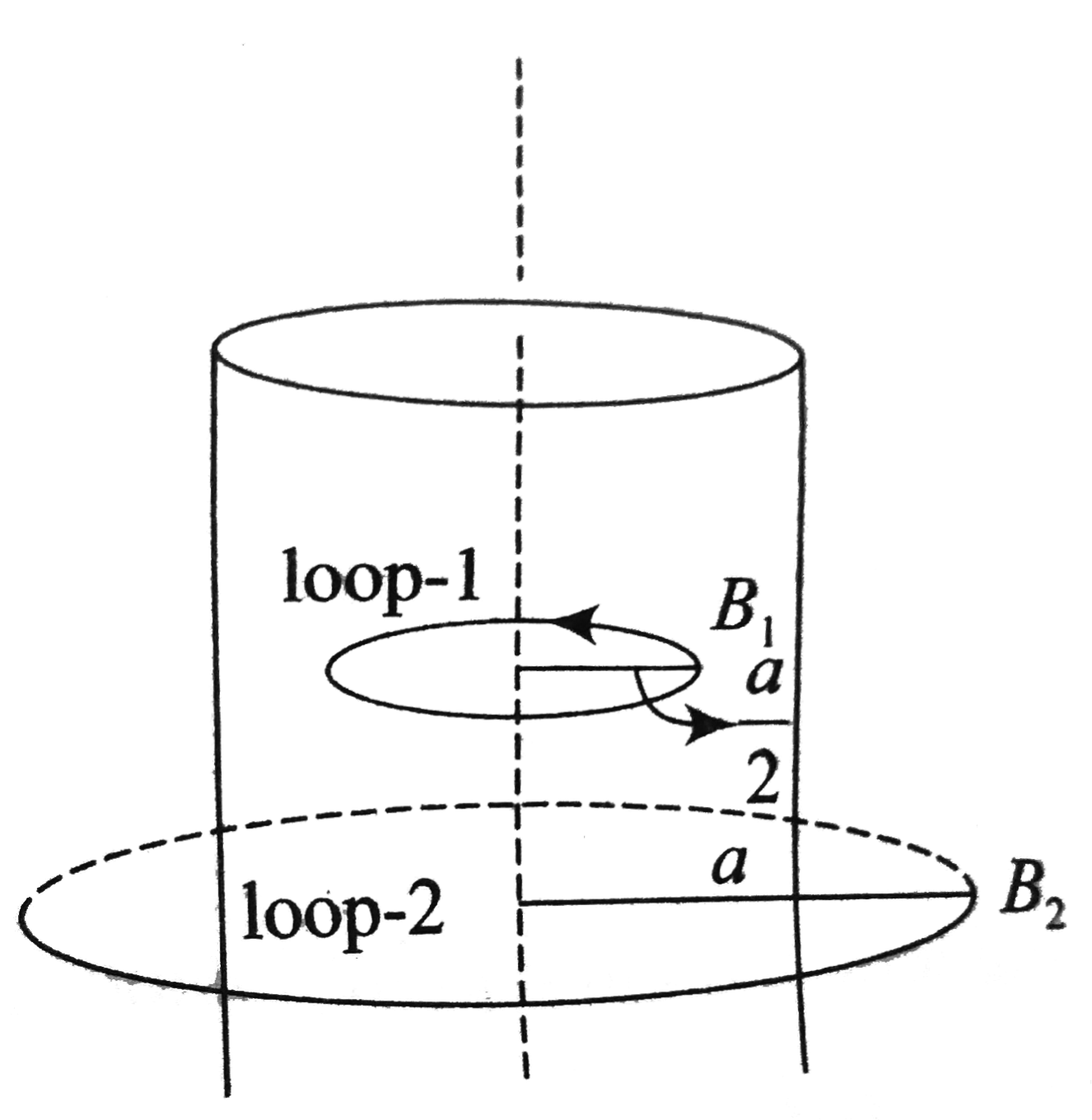
Using Ampere circuit law
For points inside the wire
Loop-1
B12πa2=μ0Iπa2×πa24
B1=μ0I4πa ....(1)
Loop-2
B2.2π2a=μ0I
⇒B2=μ0I4πa .....(2)
B1B2=1
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - AIIMS Questions
33 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Assertion- Reason
6 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning
31 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View Solution
Knowledge Check
A long straight wire of radius a carries a steady current I. The current is uniformly distributed over its cross-section. The ratio of the magnetic fields B and B' , at radial distances a2 and 2a respectively from the axis of the wire is:
A14B12C1D4A long staright wire of radius a carries a steady current I. The curent is unifromly distributed over its cross-section. The ratio of the magnetic fields B and B' , at radial distances a2 and 2a respectively from the axis of the wire is:
A14B12C1D4A long straight wire of radius a carries a steady current I. The current is uniformly distributed over its cross-section. The ratio of the inagnetic fields B and B', at radial distances a2 and 2a respectively, from the axis of the wire is
A1B4C14D12
The adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i)r<a,(ii)r>a.
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
View SolutionA long straight wire of radius 10mm carries a current uniformly distributed over its cross section. The ration of magnetic fields due to the wire at distance of 5mm and 15 mm, respectively from the axis of the wire is
View SolutionA long straight wire of radius R carries a steady current which is uniformly distributed through the cross-section of the wire. The magnitudes of the magnetic field at distance r1 and r2 from the centre of the wire are B1 and B2 respectively. Then
View Solution
