The log - log graph between the energy E of an electron and its de - Broglie wavelength λ will be
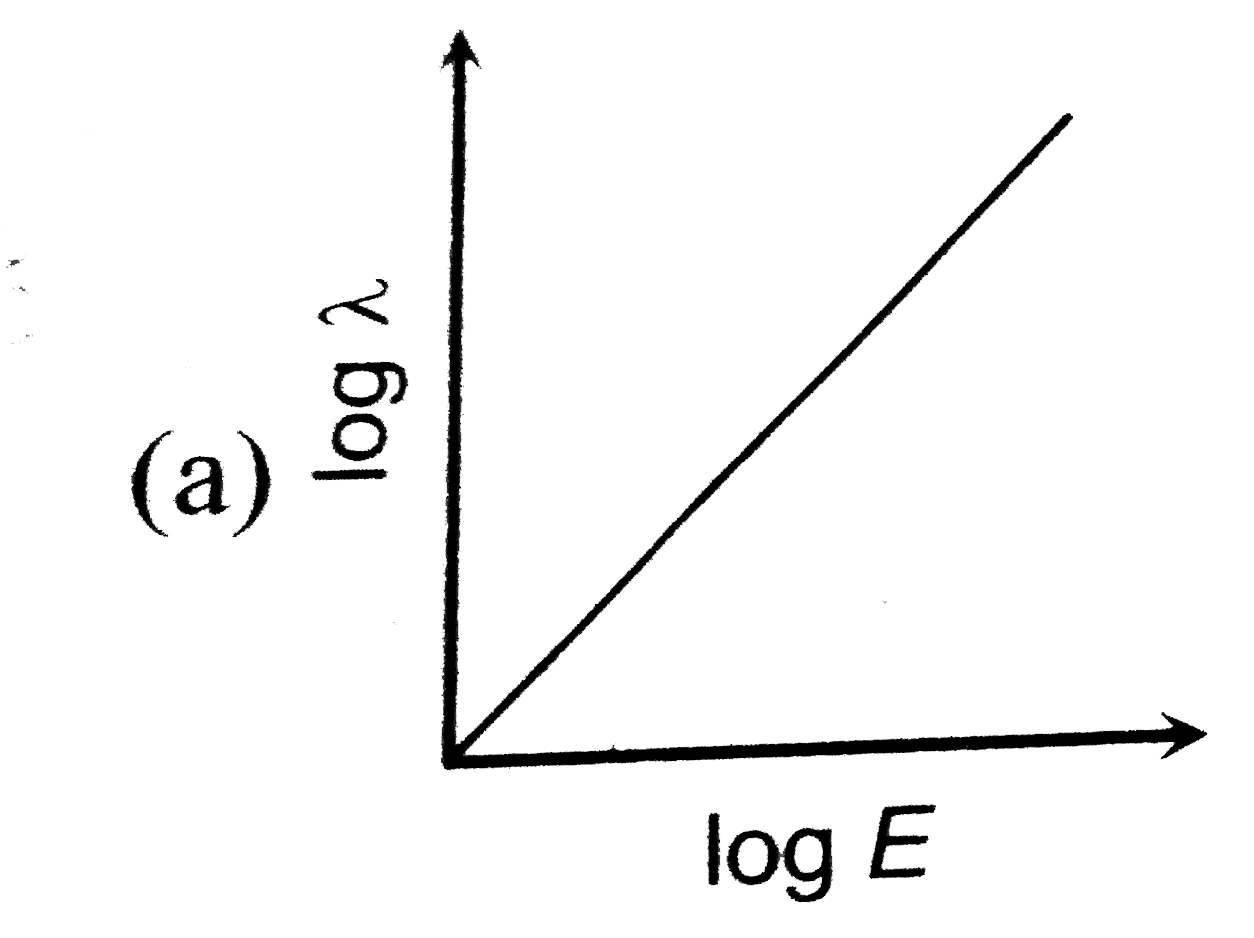
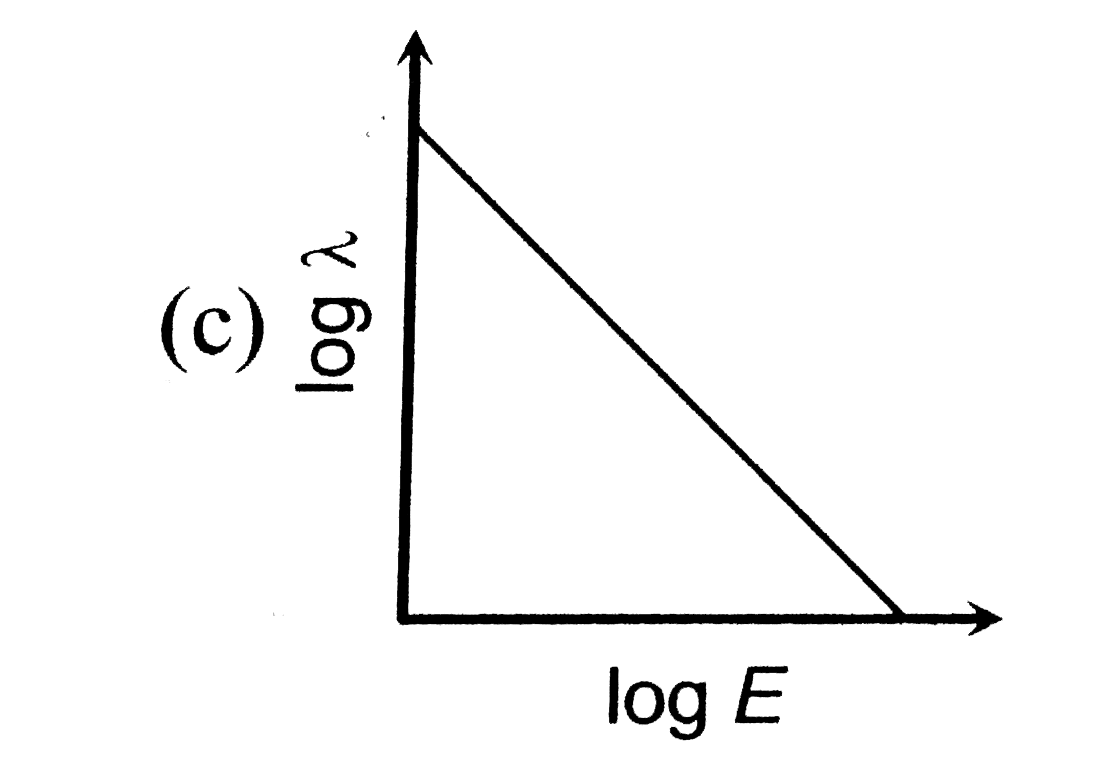
The correct Answer is:C
To analyze the relationship between the energy E of an electron and its de Broglie wavelength λ, we can start from the de Broglie wavelength formula and derive the log-log relationship step by step.
1. Understanding the de Broglie Wavelength:
The de Broglie wavelength λ of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
2. Relating Momentum to Energy:
For an electron, the momentum p can be expressed in terms of its kinetic energy E:
p=√2mE
where m is the mass of the electron.
3. Substituting Momentum into the Wavelength Formula:
By substituting the expression for momentum into the de Broglie wavelength formula, we get:
λ=h√2mE
4. Taking the Logarithm of Both Sides:
To analyze the relationship in a log-log graph, we take the logarithm of both sides:
log(λ)=log(h√2mE)
5. Applying Logarithmic Properties:
Using the properties of logarithms, we can separate the terms:
log(λ)=log(h)−log(√2m)−log(√E)
This simplifies to:
log(λ)=log(h)−12log(2m)−12log(E)
6. Rearranging the Equation:
Rearranging gives us:
log(λ)=log(h)−12log(2m)−12log(E)
This can be expressed as:
log(λ)=−12log(E)+(log(h)−12log(2m))
7. Identifying the Log-Log Graph:
In the equation log(λ)=−12log(E)+C, where C=log(h)−12log(2m), we can see that:
- The slope of the graph (in a log-log plot) is −12.
- The intercept on the y-axis is C.
Conclusion:
The log-log graph between the energy E of an electron and its de Broglie wavelength λ will have a slope of −12 and a positive intercept on the y-axis.
The de Broglie wavelength λ of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
For an electron, the momentum p can be expressed in terms of its kinetic energy E:
p=√2mE
where m is the mass of the electron.
By substituting the expression for momentum into the de Broglie wavelength formula, we get:
λ=h√2mE
To analyze the relationship in a log-log graph, we take the logarithm of both sides:
log(λ)=log(h√2mE)
Using the properties of logarithms, we can separate the terms:
log(λ)=log(h)−log(√2m)−log(√E)
This simplifies to:
log(λ)=log(h)−12log(2m)−12log(E)
Rearranging gives us:
log(λ)=log(h)−12log(2m)−12log(E)
This can be expressed as:
log(λ)=−12log(E)+(log(h)−12log(2m))
In the equation log(λ)=−12log(E)+C, where C=log(h)−12log(2m), we can see that:
- The slope of the graph (in a log-log plot) is −12.
- The intercept on the y-axis is C.
The log-log graph between the energy E of an electron and its de Broglie wavelength λ will have a slope of −12 and a positive intercept on the y-axis.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Photo Momentum Energy30videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Photo Electric Effect61videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section D - Chapter End Test29videos
CURRENT ELECTRICITY
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test29videos
ELECTRIC CHARGE, FIELD & FLUX
Similar Questions
Knowledge Check
- Question 1 - Select One
de-Broglie wavelength λ is
Aproportional to massBproportional to impulseCinversely proportional to impulseDindependent to impulse - Question 2 - Select One
The de Broglie wavelength λ of a particle
Ais proportional to massBis proportional to impluseCis inversely proportional to impulseDdoes not depend on impulse - Question 3 - Select One
The de Broglie wavelength λ of a particle
Ais proportional to massBis proportional to impluseCis inversely proportional to impulseDdoes not depend on impulse
The kinetic energy of an electron with de-Broglie wavelength of 3 nm is :
View SolutionThe kinetic energy of an electron with de-Broglie wavelength of 3 nm is :
View SolutionThe kinetic energy of an electron with de - Broglie wavelength of 0.3nanometre is
View SolutionIn an excited state of hydrogen like atom an electron has total energy of −3.4eV. If the kinetic energy of the electron is E and its de-Broglie wavelength is λ, then
View SolutionThe energy that should be added to an electron to reduce its de Broglie wavelength from λ to λ2 is (Considering E to the energy of electron when its de Broglie wavelength is λ )
View Solution

