A long straigth wire of resistance , radius and length carries a constant current .The poynting vector for the wire will be
The correct Answer is:d
To find the Poynting vector S for a long straight wire of resistance R, radius a, and length l carrying a constant current I, we can follow these steps:
1. Understand the Poynting Vector:
The Poynting vector S represents the power per unit area carried by an electromagnetic wave and is given by the formula:
S=1μ0E×B
where E is the electric field and B is the magnetic field.
2. Determine the Electric Field E:
For a long straight wire carrying a current I, the electric field E at a distance r from the wire can be calculated using Ohm's law. The potential difference V across the length l of the wire is given by:
V=I⋅R
The electric field E is then:
E=Vl=IRl
3. Determine the Magnetic Field B:
The magnetic field around a long straight wire carrying current I can be calculated using the Biot-Savart law. At a distance r from the wire, the magnetic field B is given by:
B=μ0I2πr
4. Calculate the Poynting Vector S:
Substitute the expressions for E and B into the Poynting vector formula:
S=1μ0(IRl)×(μ0I2πa)
Simplifying this gives:
S=IR⋅I2πl=I2R2πl
5. Final Expression:
The final expression for the Poynting vector S is:
S=I2R2πl
The Poynting vector S represents the power per unit area carried by an electromagnetic wave and is given by the formula:
S=1μ0E×B
where E is the electric field and B is the magnetic field.
For a long straight wire carrying a current I, the electric field E at a distance r from the wire can be calculated using Ohm's law. The potential difference V across the length l of the wire is given by:
V=I⋅R
The electric field E is then:
E=Vl=IRl
The magnetic field around a long straight wire carrying current I can be calculated using the Biot-Savart law. At a distance r from the wire, the magnetic field B is given by:
B=μ0I2πr
Substitute the expressions for E and B into the Poynting vector formula:
S=1μ0(IRl)×(μ0I2πa)
Simplifying this gives:
S=IR⋅I2πl=I2R2πl
The final expression for the Poynting vector S is:
S=I2R2πl
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Communication System61videos
ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Problems Based On Mixed Concepts39videos
ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC INDUCTION
- BOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Section D - Chapter End Test30videos
GEOMETRICAL OPTICS
Similar Questions
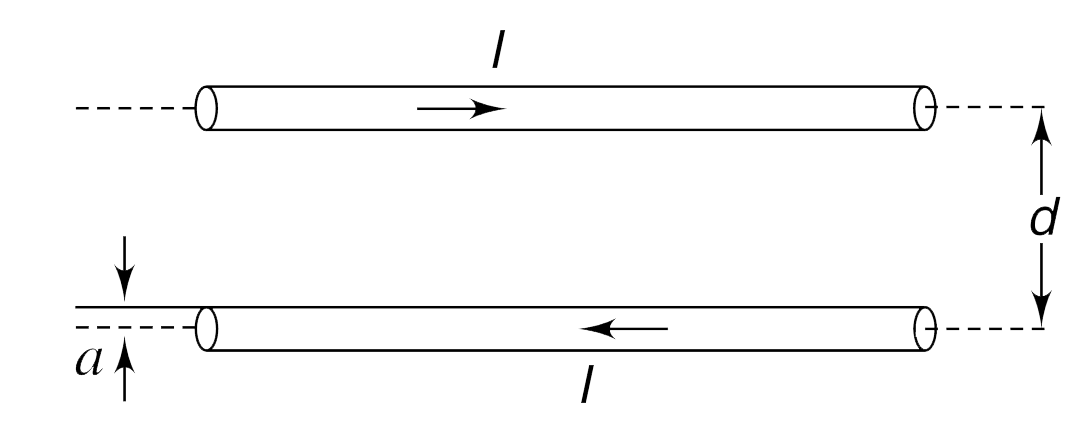
A long straight wire of cross sectional radius a carries a current I. The return current is carried by an identical wire which is parallel to the first wire. The centre to centre distance between the two wires is d. Find the inductance (L) of a length x of this arrangement. Neglect magnetic flux inside the wires.
 View Solution
View SolutionWrite Ampere's circuital law.A long straight wire of a circular cross section (radius a) carrying steady current.Current is uniformly distributed in the wire.Calculate magnetic field inside the region (r<a) in the wire.
View Solution
Knowledge Check
- Question 1 - Select One
An electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
Acurrent I will decreaseBcurrent I will increaseCresistance R will increaseDresistance R will decrease - Question 2 - Select One
An electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
Acurrent I will decreaseBcurrent I will increaseCresistance R will increaseDresistance R will decrease - Question 3 - Select One
In Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).

The emf induced in the closed loop isAμ0I0a2πIn(2a+ll)Bμ0I0a2πIn(2a−ll)Cμ0I0aπIn(a+ll)Dμ0aπIn(a+ll)
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
 View Solution
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a
 View Solution
View SolutionTwo infinitely long straight wires lie in the xy-plane along the lines x=±R. The wire located at x=+R carries a constant current I1 and the wire located at x=−R carries a constant current I2. A circular loop of radius R is suspended with its centre at (0,0,√3R) and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the +ˆJ direction. Which of the following statements regarding the magnetic field →B is (are) true?
View SolutionCalculate the force per unit length on a long straight wire carrying current of 4 A due to a parallel wire carrying 6 A current . Distance between the wires is 3 cm.
View SolutionIn Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).
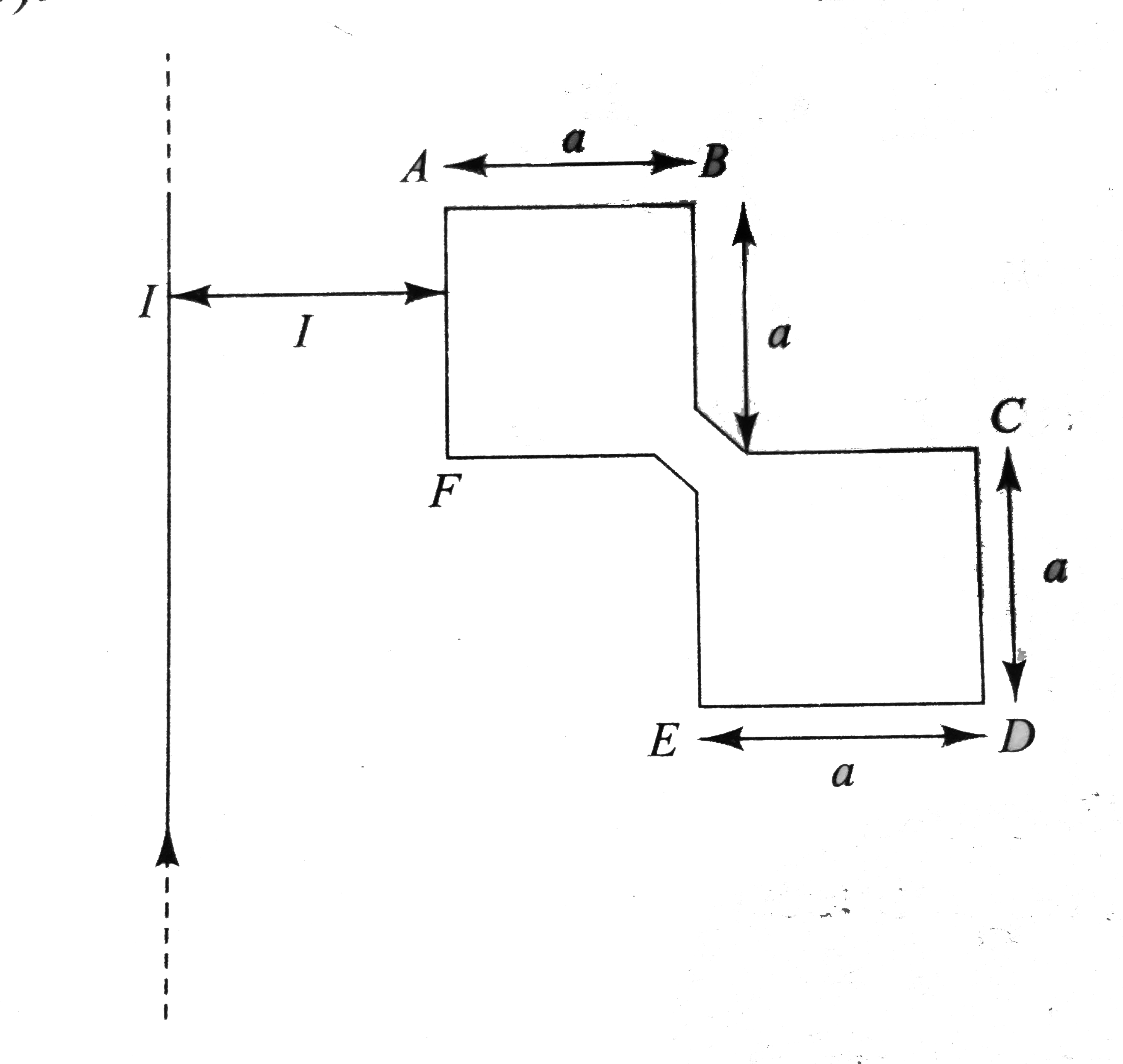
The heat produced in the loop in time t isView Solution

