Select the correct statements for ideal gases:
1.(∂H∂T)P−(∂U∂T)V=R
2.(∂H∂T)P−(∂U∂T)P−(∂U∂T)V=work done
3.(∂U∂V)T=+ve
4.(∂T∂P)H=+ve
1,2,3,4
1,2,4
1,2,3
1
The correct Answer is:A
Step by step video, text & image solution for Select the correct statements for ideal gases: 1. ((delH)/(delT))_(P)-((delU)/(delT))_(V)=R 2. ((delH)/(delT))_(P)-((delU)/(delT))_(P)-((delU)/(delT))_(V)=work done 3. ((delU)/(delV))_(T)=+ve 4. ((delT)/(delP))_(H)=+ve by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Assertion: CP−CV=R for an ideal gas.
Reason: (∂E∂V)T=0 for an ideal gas.AStatement 1 is true, statement-2 is true, statement 2 is a correct explanation for statement 6BStatement 1 is true, statement 2 is true, statement 2 is not a correct explanation for statement 6CStatement 1 is true, statement 2 is falseDStatement 1 is false, statement 2 is trueAssertion: The coefficient of isothermal expansion at critical point is zero.
Reason: (∂Vc∂Tc)Pc=0AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.The temperature coefficient of the cell is (∂E∂T)P. Choose the correct statements (s).
AWhen (∂E∂T)P=0 , then ΔH=−nFEBWhen (∂E∂T)P<0, then |nFE|>|ΔH|CWhen (∂E∂T)P>0, then |nFE|<|ΔH| Exothermic reactionDWhen (∂E∂T)P=0, then |ΔH|>|nFE| Endothermic reaction.
Assertion: Ideal gas does not show Joule-Thomson effect as well as they cannot be liquefied.
Reason: (∂E∂V)T and (∂T∂P)H for ideal gas is zero.
View SolutionWith the help of fthermondynamic equation of state
(∂U∂V)T=T(∂P∂T)V−P
Answer the following questions for a van der Waals' gas
P=nRTV−nb−an2V2
Work done for the isothermal process from (P1V1T1 to (P2V2T) is :
View SolutionWith the help of fthermondynamic equation of state
(∂U∂V)T=T(∂P∂T)V−P
Answer the following questions for a van der Waals' gas
P=nRTV−nb−an2V2
Work done for the isothermal process from (P1V1T) to (P2V2T) is :
View SolutionConsider a wave sent down a string in the positive direction whose equation is given is
y=y0sin[ω(t−xv)]
The wave is propagated along because each string segment pulls upward and downward on the segment adjacent to it a slightly larger value of x and, as a result does work upon the string segment to which wave is travelling.
For example, the portion of string at point A is going upward, and will pull the portion at point B upward as well. In fact, at any point along the string, each segment of the string is pulling on the segment just adjacent and to its right, causing the wagve to propagate. It is by this process that the energy is sent along the string.
Now we try to calculate how much energy is propagated down the stirng per second
Ty=tsinθ≈Ttanθ⇒Ty=−T∂y∂x
(The negative sign appears because as shown in the figure II, the slope is negative) the force will act through a distance
dy=vydt=∂y∂tdt
Therefore work done by force in time dt is
dW=Tydy=−T(∂y∂x)(∂y∂t)dt⇒dW=ω2y20Tvcos2[ω(t−xV)]dt.....(A)
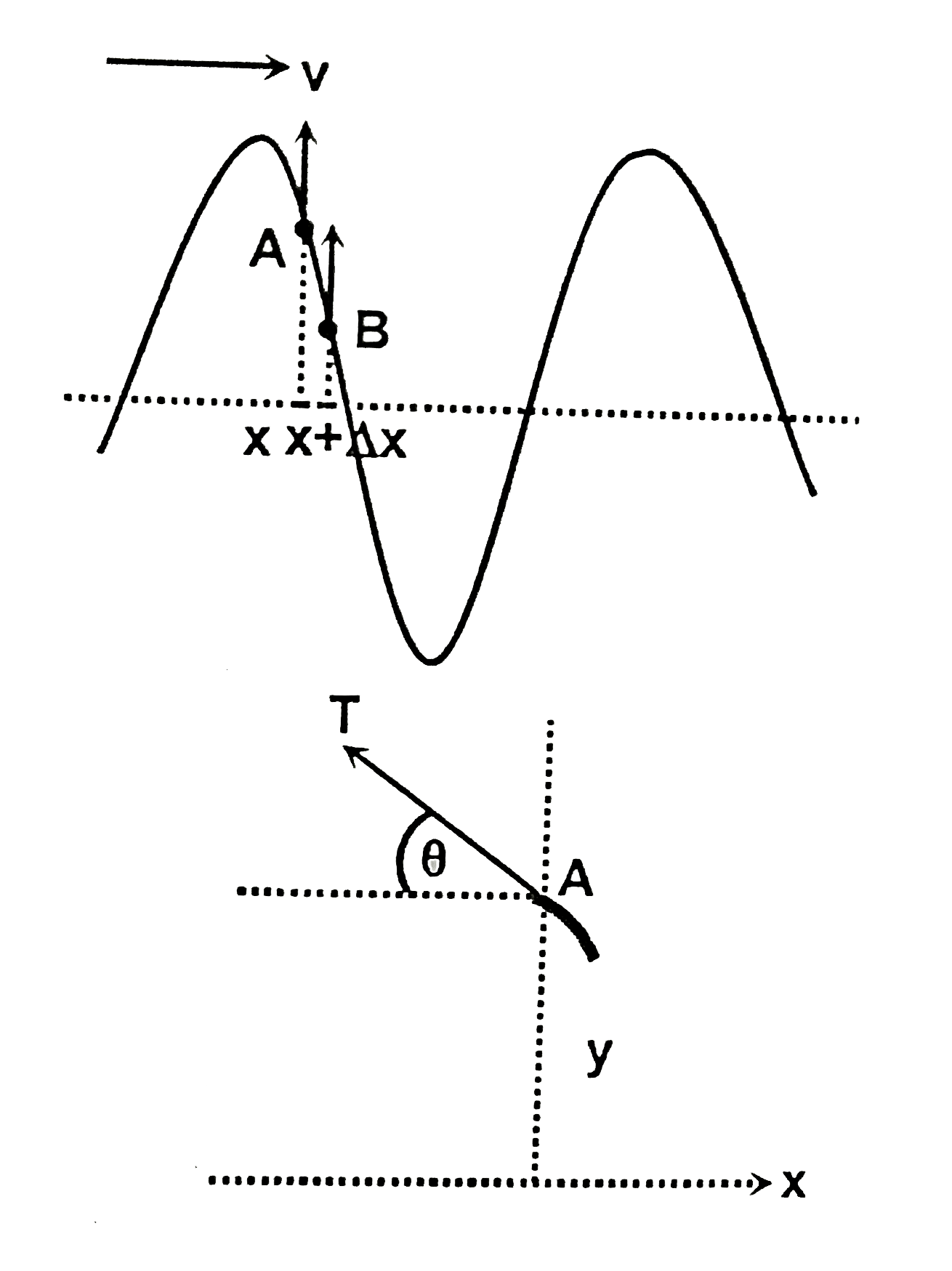
The average power transmitted down the string (i.e. the average energy transfer or sent down it per second) is
View SolutionWith the help of fthermondynamic equation of state
(∂U∂V)T=T(∂P∂T)V−P
Answer the following questions for a van der Waals' gas
P=nRTV−nb−an2V2
ΔH for the insothermal process from (P1V1T)to (P2V2T) to is :
View Solution
