Two equal masses of $6.40 k g$ are separted by a distance of $0.16 m$ . A small body is released from a point $P$ , equidistant from the two masses and at a distance of $0.06 m$ from the line joining them. Fig.
(a) Calculate the velocity of this body when it passes through $Q$ .
(b) Calculate the acceleration of this body at $P$ and $Q$ if its mass is $0.1 k g$ .
Use $G = 6.67 \times 10^{- 11} N m^{2} k g^{- 2}$

Video Solution

Text Solution

Verified by Experts

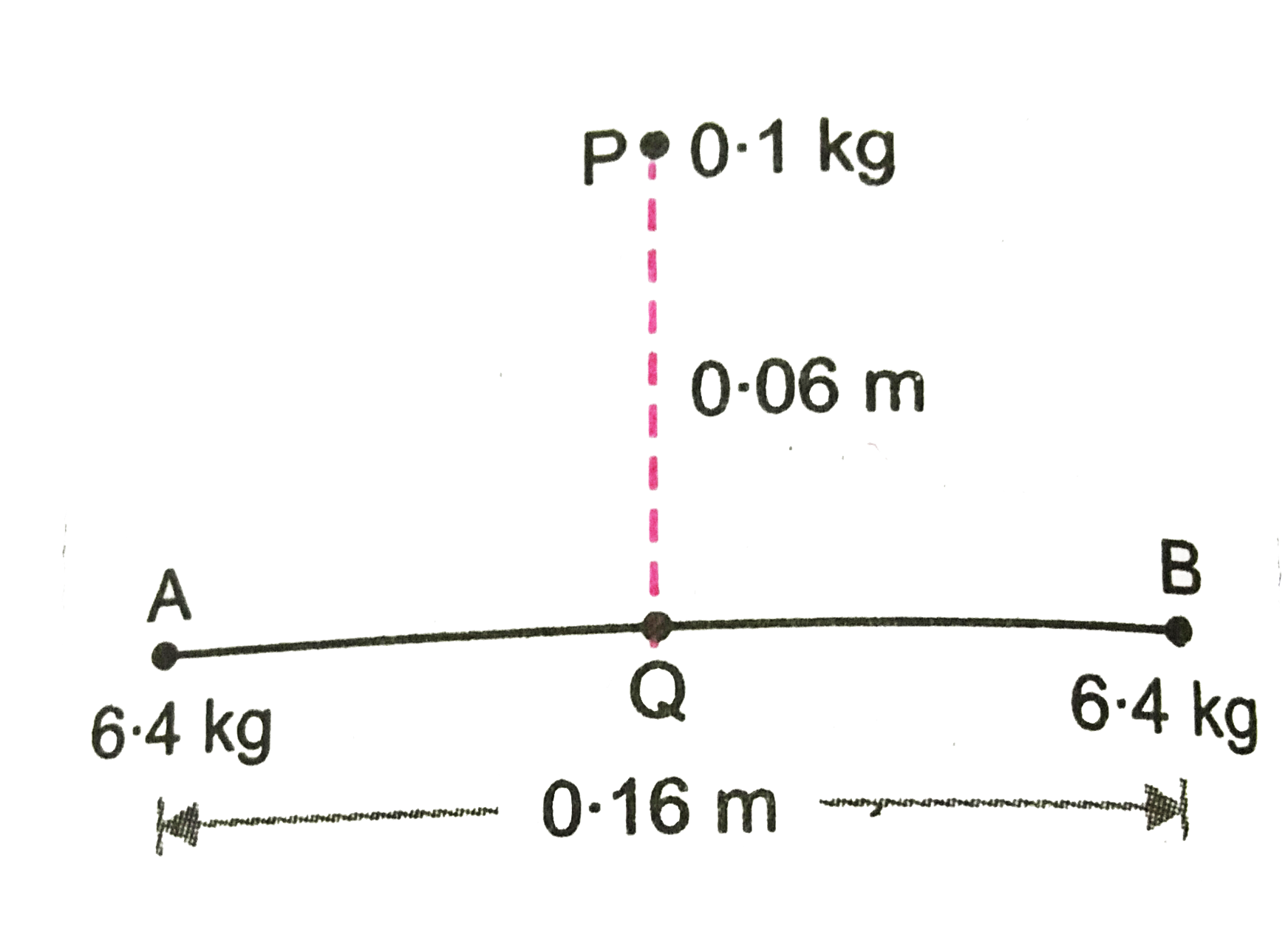
In figure, $A P = B P = \sqrt{{(0.08)}^{2} + {(0.06)}^{2}} = 0.1 m$
Here, $m_{1} = 6.4 k g = m_{2}$ and $m_{3} = 0.1 k g$
(a) When body falls from $P$ to $Q$ , then gain in $K E$ of body is equal to loss in $P E$ of the system.
$∴ \frac{1}{2} m_{3} υ^{2} = - [\frac{G m_{1} m_{3}}{(0.1)} + \frac{G m_{2} m_{3}}{0.1}]$
$+ [\frac{G m_{1} m_{3}}{0.08} + \frac{G m_{2} m_{3}}{0.08}]$
or $\frac{1}{2} υ^{2} = - [\frac{G m_{1}}{0.1} + \frac{G m_{2}}{0.1}] + [\frac{G m_{1}}{0.08} + \frac{G m_{2}}{0.08}]$
or $υ^{2} = - 2 \times G [(\frac{6.4}{0.1} + \frac{6.4}{0.1}) - (\frac{6.4}{0.08} + \frac{6.4}{0.08})]$
$= - 2 \times (6.67 \times 10^{- 11}) \times (- 32)$
$= 64 \times 6.67 \times 10^{- 11}$
or $υ = {(64 \times 6.67 \times 10^{- 11})}^{1 / 2} = 6.53 \times 10^{- 5} m s^{- 1}$

Updated on:21/07/2023