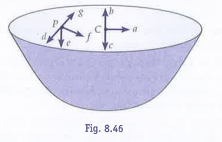
The gravitation intensity at the centre C of the
drumhead defined by a hemispherical shell has the direction
indicated by the arrow [see Fig. 8.46]
![The gravitation intensity at the centre C of the
drumhead defined by a hemispherical shell has the direction
indicated by the arrow [see Fig. 8.46]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DRC_SLA_PHY_XI_P1_C08_S27_020_Q01.png)
We know that the gravitational potential is constant at all points inside a spherical shell. Therefore, the gravitational potential gradient at all points inside the spherical shell is zero [i.e., as V is constant, dVdr=0].
Since, gravitational intensity is equal to negative of the gravitational potential gradient, hence the gravitational intensity is zero at all points inside a hollow spherical shell.
This indicates that the gravitational forces acting on a particle at any point inside a spherical shell, will be symmetrtically placed.
Therefore. if we remove the upper hemispherical shell, the net gravitational force acting on the particle at the centre Q or at some other point P will be acting downwards which will also be the direction of gravitational intensity. it is so because, the gravitational intensity at a point is the gravitational force per unit mass at that point. Hence, the gravitational intensity at the centre Q will be also c.i.e., option (iii) is correct.
Topper's Solved these Questions
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - ADDITIONAL EXERCISES
4 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - VERY SHORT ANSWER QUESTIONS
11 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - ADVANCED PROBLEMS FOR COMPETITIONS
15 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions
14 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
Similar Questions
The gravitation intensity at the centre C of the drumhead defined by a hemispherical shell has the direction indicated by the arrow [see Fig. 8.46]
View SolutionIn the following two exercises, choose the correct answer from among the given ones: The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig.) (i) a, (ii) b, (iii) c, (iv) 0.

View Solution
Knowledge Check
The direction of gravitational intensity at point P of a hemispherical shell of uniform mass desity is indicated by the arrow
 AdBeCfDg
AdBeCfDgThe electric field intensity at the center of a uniformly charged hemispherical shell is E0. Now two portions of the hemisphere are cut from either side, and the remaining portion is shown in fig. If α=β=π/3, then the electric field intesity at the center due to the remaining portion is
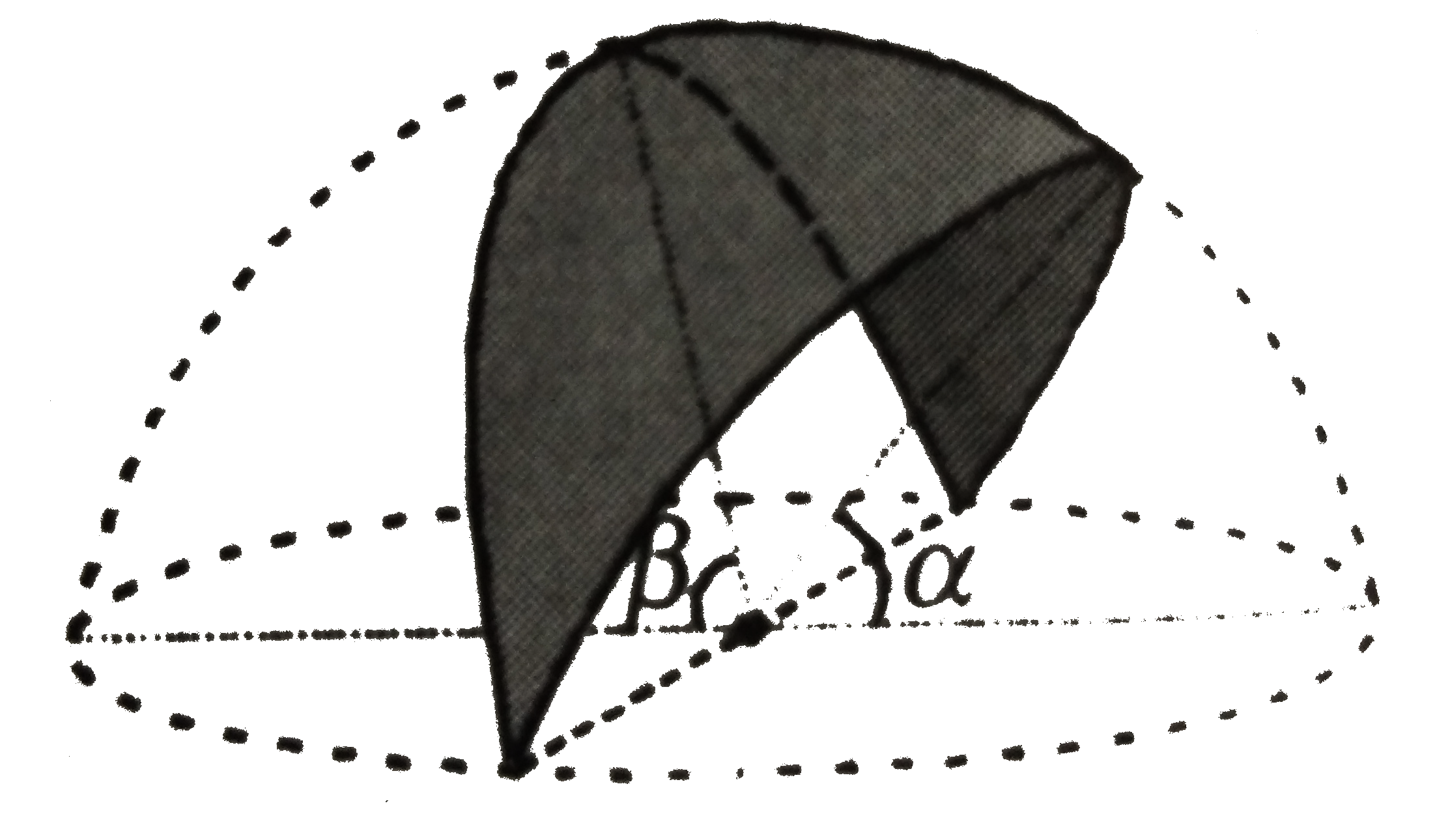 AE0/3BE0/6CE0/2Dinformation insuffiecient
AE0/3BE0/6CE0/2Dinformation insuffiecientWhat is the intensity of gravitational field of the centre of a spherical shell
AGm/r2BgCZeroDNone of these
Calculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass M and radius R. (Assume the base of hemisphere to be open)

View SolutionCalculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View SolutionIf gravitational field Intensity is E at distance R/2 outside from then surface of a thin shell of radius R , the gravitational field intensity at distance R/2 from its centre is
View SolutionThe gravitational field intensity at a point 10,000km from the centre of the earth is 4.8Nkg−1. The gravitational potential at that point is
View SolutionLet S be an imaginary closed surface enclosing mass m. Let d→S be an element of area on S, the direction of d→S being outward from S. Let →E be the gravitational intensity at d→S. We define ϕ=∮sE⋅dS, the integration being carried out over the entire surface S.
View Solution
