Question

Find the intensity of gravitational field at a point lying at a distance $x$ from the centre on the axis of a ring of radius $a$ and mass $M$.

Explanation

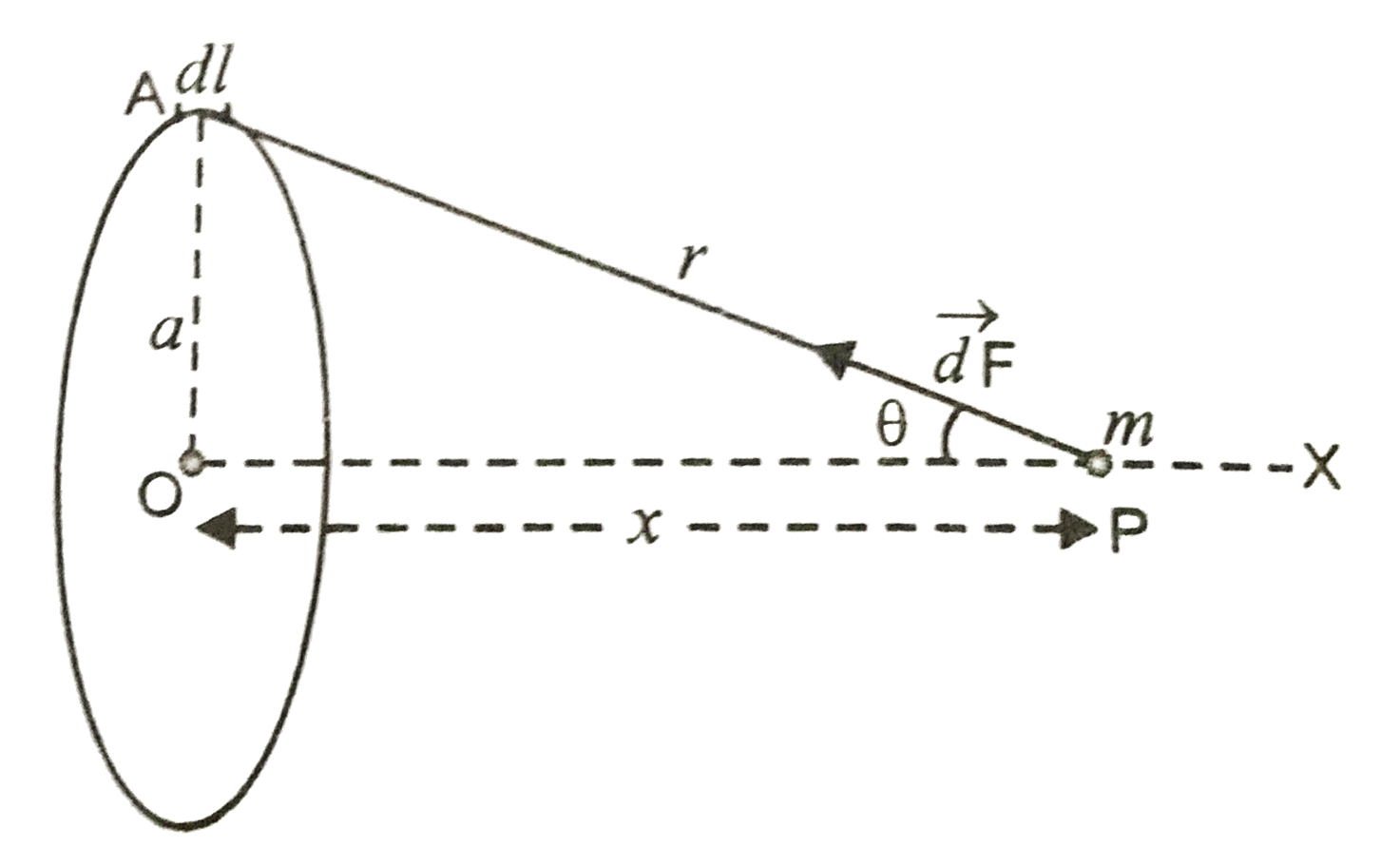
Consider a ring of mass `M`, radius a with centre at `O`. Mass per unit length of ring `= (M)/(2 pi a)`. Let `P` be a point on the axis of ring at a distance `x` from `O` as shown in Fig. Take an element of length `dl` of the ring.
Mass of this element of the ring, `dM = (M)/(2 pi a) xx dl`.
Gravitational force on the particle of mass `m` at `P` due to this element is
`dF = (GmdM)/(r^(2)) = (Gm(M//2 pi a)dl)/(r^(2))`
acting along `PA` where, `r = PA = (a^(2) + x^(2))^(1//2)`
Resolving `d vecF` into two rectangular components, we get, `dF cos theta` acts along the axis directed towards `O` and `dF sin theta` acts perpendicular to axis.
now we calculate the force on the particle at `P` due to all elements of the ring and divide these forces into two rectangular components, along the axis and the perpendicular to the axis of ring. We note that the component of forces perpendicular to the axis due to all elements will cancel each other and component of forces along the axis will add up. So the resultant gravitational force on particle at `P` due to all element is
`F = int dF cos theta = (GmM)/(2 pi a) int (dl)/(r^(2))((x)/(r))`
`= (GmMx)/(2pi a(a^(2) + x^(2))^(3//2)) int dl = (GmMx)/(2pi a(a^(2) + x^(2))^(3//2)) xx 2pi a = (GmMx)/((a^(2) + x^(2))^(3//2))`
Gravitational intensity at `P` is, `I = (F)/(m) = (GMx)/((a^(2) + x^(2))^(3//2))`
In vector from, `underset(T)rarr = - (GMx)/((a^(2) + x^(2))^(3//2))hatx`,
where -ve sign shown that the graviational intensity is of attractive field.