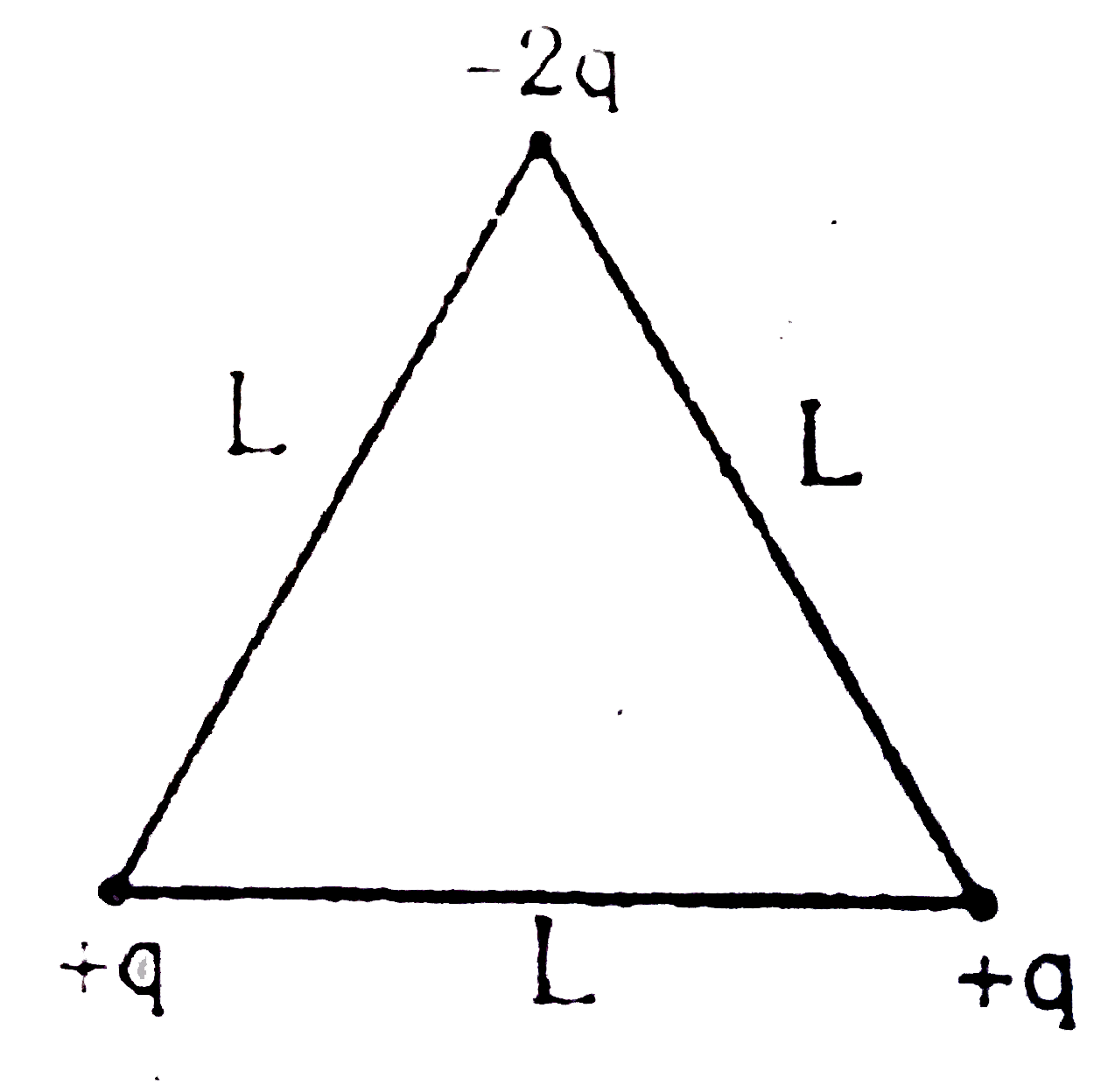
Three point masses are at the corners of an equilateral traingle of side r. Their separations do not change when the system rotates about the centre of the triangle. For this, the time period of rotation must be proportional to
r3/2
r
m
m−1/2
The correct Answer is:A, D
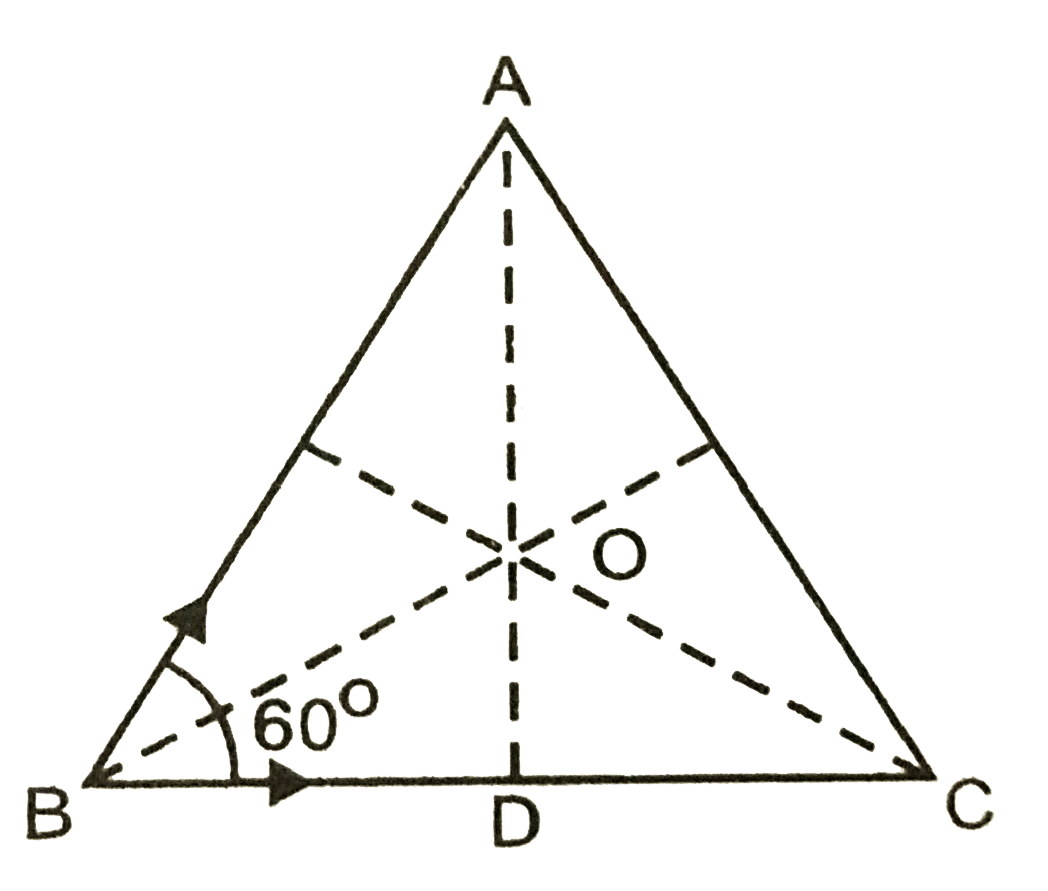
Refer to Fig. O is the centre of mass of the system of 3 particles present at A,B and C
repectively. Here AD=ABsin60∘=r√3/2
OA=23AD=23×r√32=r3=OB=OC
Gravitational force on the particle at B due to
particle at C is FBC=Gm×mr2 along BC
Gravitational force on the particle at B due to
particle at A is FBA=GM×mr2 along BA
The resultant force on particle at B will act along BO is
F=√G2m4r4+G2m4rr+2Gm2r2×Gm2r2cos60∘
This force is providing the centripetal force, so
√3Gm2r2=mr√34π2T2
or T=√4π2r33Gm or T∝√r3m
Similar Questions
Knowledge Check
Three charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
A18×10−6JB9JC9×10−6JD27JThree point masses, each of mass m, are placed at the corners of an equilateral triangle of side L. The moment of inertia of this system about an axis along one side of the triangle is
AmL2B3mL24C3mL2D3mL22Three point masses, each of mass m, are placed at the corner of an equilateral triangle of side 1. Then the moment of inertia of this system about an axis along one side of the triangle is
A3ml2Bml2C34ml2D32ml2
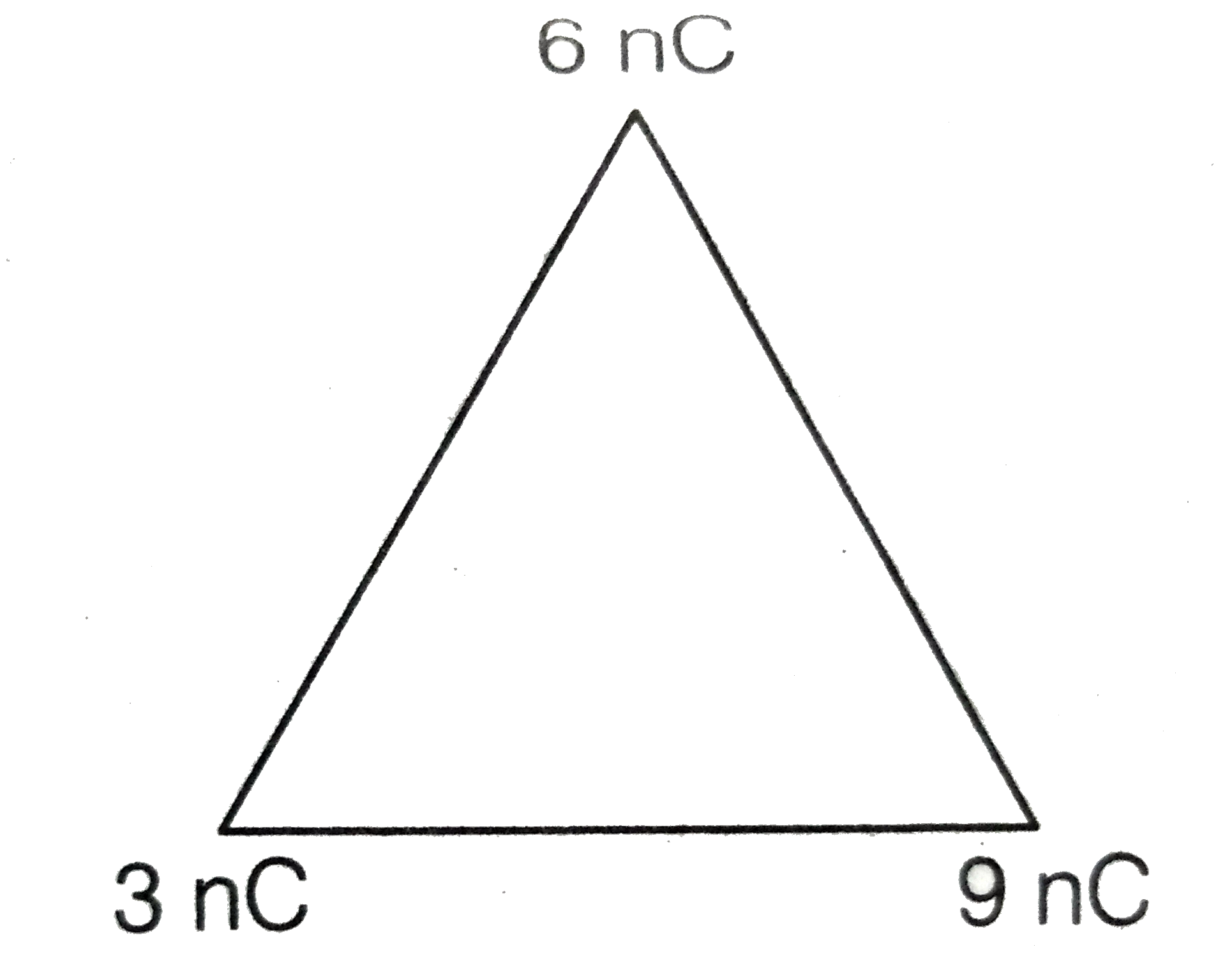
Three point charges 3nC, 6nC and 6nC are placed at the corners of an equilateral triangle of side 0.1 m. The potential energy of the system is
View SolutionThree equal masses (each m) are placed at the corners of an equilateral triangle of side a'. Then the escape velocity of an object from the circumcentre P of triangle is
View SolutionThree equal masses (each m) are placed at the corners of an equilateral triangle of side a. Then the escape velocity of an object from the circumcentre P of triangle is
View SolutionThree point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is
View SolutionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
View Solution