The ratio stress/strain remains constant for small deformation. What will be the effect on this ratio when the deformation made is very large?
When the deforming force is applied beyond elastic limit, the strain produced is more than that has been observed within elastic limit. Due to it, the ratio stress/strain will decrease.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Short Answer Questions162videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Long Answer questions33videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Curiosity Questions9videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The ratio of stress to strain is called
AFrictional coefficient,BElastic constant,CCoefficient of viscosity,DSurface tension. - Question 2 - Select One
The ratio of stress and strain is called
Asurface tensionBmodulus of elasticity,Ccoefficient of friction,Dcoefficient of viscosity. - Question 3 - Select One
When total revenue is constant, what will be the effect on average revenue ?
AAR will fallBAR will increaseCAR will also be constantDNo effect on AR
What is the effect on MR when TR increases at constant
View SolutionIn the diagram shown, no friction at any contact surface. Initially, the spring has no deformation. What will be the maximum deformation in the spring ? Consider all the strings to be sufficiency large. Consider the spring constant to be K.
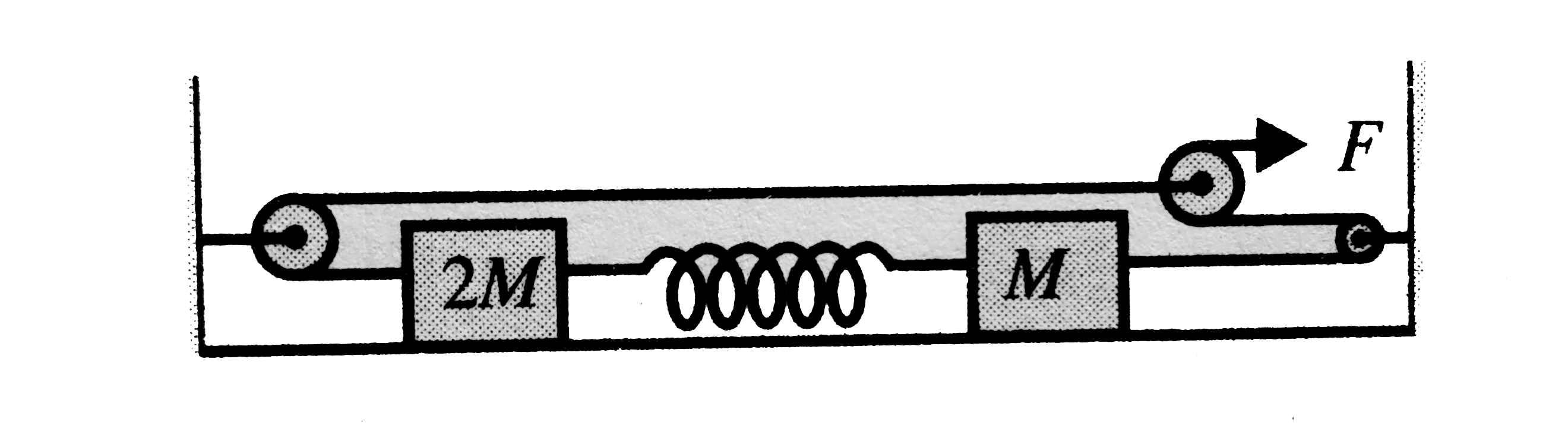 View Solution
View SolutionIn the diagram shown, no friction at any contact surface. Initailly, the spring has no deformation .What will be the maximum deformation in the spring? Consider all the strings to be sufficiently large. Consider the spring constant to be K.
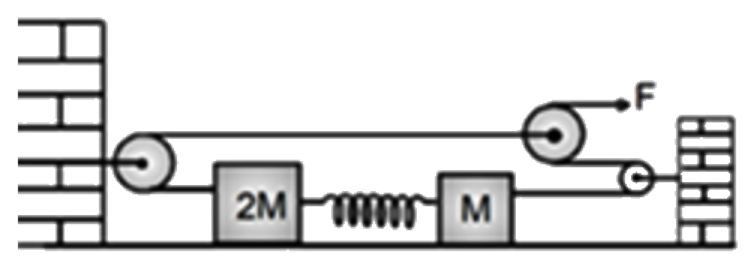 View Solution
View SolutionStress to strain ratio is equivalent to
View SolutionThe ratio of shearing stress to the shearing strain is defined as
View Solution

