Water at a pressure of 4×104Nm−2 flows at 2ms−1 through a horizontal pope of 0.02m2. What is the pressure in the smaller cross-section of the pipe?
To solve the problem of finding the pressure in the smaller cross-section of the pipe, we can use the principle of conservation of mass (continuity equation) and Bernoulli's equation.
1. Identify Given Data:
- Initial pressure P1=4×104N/m2
- Initial velocity V1=2m/s
- Cross-sectional area of the larger section A1=0.02m2
- Cross-sectional area of the smaller section A2=0.01m2
2. Use the Continuity Equation:
The continuity equation states that the product of the cross-sectional area and the velocity is constant along the pipe:
A1V1=A2V2
Rearranging gives:
V2=A1V1A2
Substituting the known values:
V2=0.02×20.01=4m/s
3. Apply Bernoulli's Equation:
Bernoulli's equation for two points in a flowing fluid is given by:
P1+12ρV21=P2+12ρV22
Rearranging to find P2:
P2=P1+12ρV21−12ρV22
4. Substitute Values into Bernoulli's Equation:
We need the density ρ of water, which is approximately 1000kg/m3.
P2=4×104+12×1000×(22)−12×1000×(42)
Calculating the kinetic energy terms:
P2=4×104+12×1000×4−12×1000×16
P2=4×104+2000−8000
P2=4×104−6000
P2=34000N/m2
5. Final Answer:
The pressure in the smaller cross-section of the pipe is:
P2=3.4×104N/m2
- Initial pressure P1=4×104N/m2
- Initial velocity V1=2m/s
- Cross-sectional area of the larger section A1=0.02m2
- Cross-sectional area of the smaller section A2=0.01m2
The continuity equation states that the product of the cross-sectional area and the velocity is constant along the pipe:
A1V1=A2V2
Rearranging gives:
V2=A1V1A2
Substituting the known values:
V2=0.02×20.01=4m/s
Bernoulli's equation for two points in a flowing fluid is given by:
P1+12ρV21=P2+12ρV22
Rearranging to find P2:
P2=P1+12ρV21−12ρV22
We need the density ρ of water, which is approximately 1000kg/m3.
P2=4×104+12×1000×(22)−12×1000×(42)
Calculating the kinetic energy terms:
P2=4×104+12×1000×4−12×1000×16
P2=4×104+2000−8000
P2=4×104−6000
P2=34000N/m2
The pressure in the smaller cross-section of the pipe is:
P2=3.4×104N/m2
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Conceptual Problems103videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions21videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Long Answer questions33videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
Similar Questions
Water is flowing with a speed of 2m/s in a horizontal pipe with cross-sectional area decreasing from 2×10−2m2 to 0.01m2 at pressure 4×104 pascal. What will be the pressure at smaller cross-section?
View SolutionThe cross sectional area of a horizontal pipe is decreasing from 5×10−2m2 to 1×10−2m2?. Water is flowing with speed of 5 m/s through this pipe with a pressure of 5×105Pa through the larger cross section. The pressure at the smaller cross section of the pipe is n×104Pa. Find the value of n.
View Solution
Knowledge Check
- Question 1 - Select One
Water is flowing steadily through a horizontal pipe of non-uniform cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2m/s. What is the pressure at a point where cross-section reduces to 0.01m2 ?
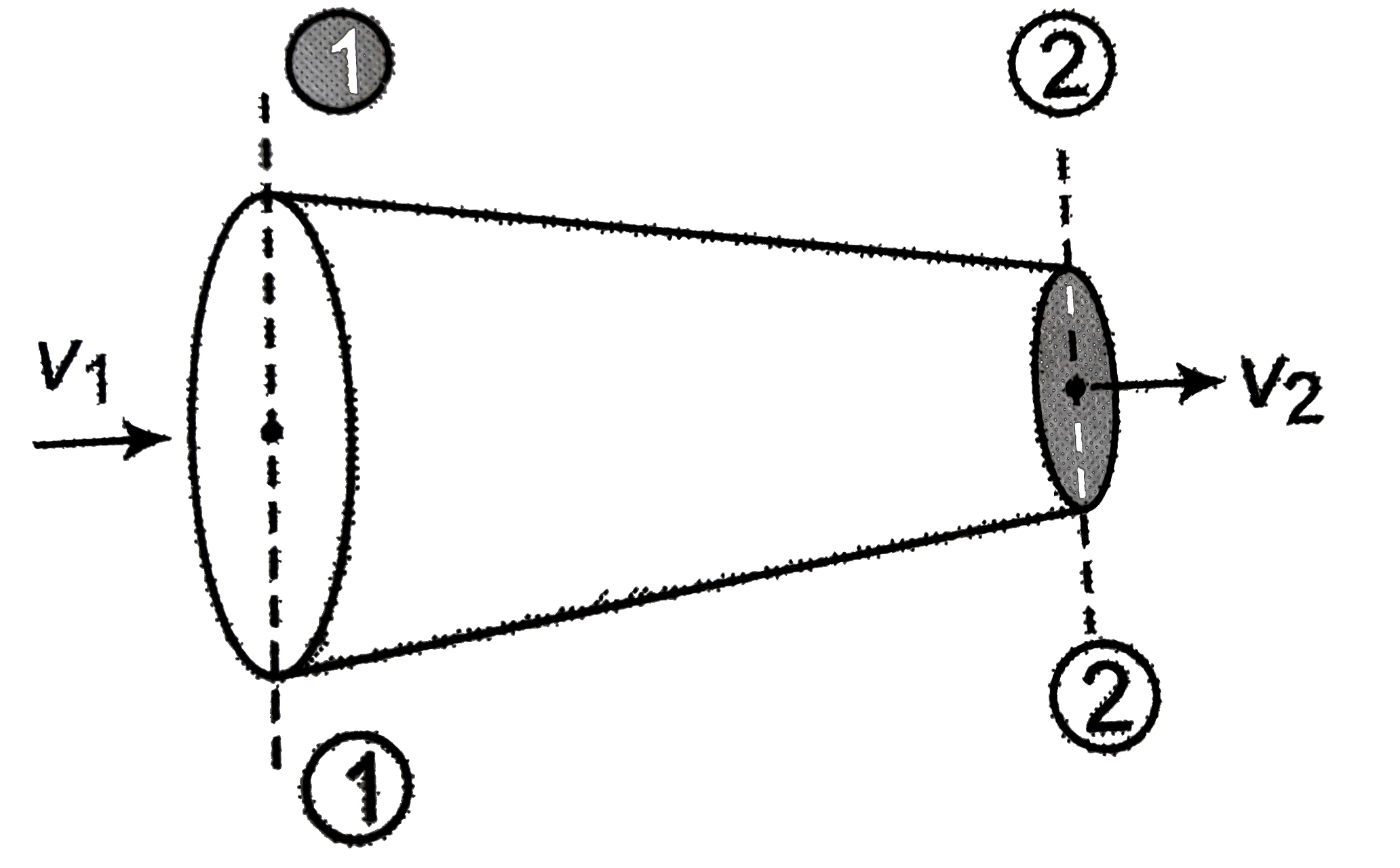 .A1.4×104N/m2B3.4×104N/m2C2.4×10−4N/m2Dnone of these
.A1.4×104N/m2B3.4×104N/m2C2.4×10−4N/m2Dnone of these - Question 2 - Select One
Water is flowing through a horizontal pipe of non-uniform cross- section. At the extreme narrow portion of the pipe, the water will have
AMaximum speed and least pressureBMaximum pressure and least speedCBoth pressure and speed maximumDBoth pressure special least
Water is flowing steadily through a horizontal pipe of non-uniform cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2m/s. What is the pressure at a point where cross-section reduces to 0.01m2 ?
 .View Solution
.View SolutionWater flowing steadily through a horizontal pipe of non-unifrom cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2ms−1 . The pressure at a point where cross-section reduces to 0.01m2 is 3.4×10n Pa. What is the value of n ?
View SolutionThe cross-sectional area of water pipe entering the basement is 4cm−2 . The pressure at the point is 3.5×105Nm−2 and the speed of water is 2.2ms−1 . This pipe tapers to a cross-sectional area of 2cm2 when it reaches the second floor 10 m above . Calculate the speed and pressure at the second floor. use g=10m/s2.
View SolutionWater is moving with a speed of 5.0 m/s through a pipe with a cross-sectional area of 4.0cm2. The water gradually descends 12 m as the pipe cross-sectional area increases to 8.0cm2 (a) What is the speed at the lower level? (b) If the pressure at the upper level is 1.5×105 Pa, what is the pressure at the lower level?
View SolutionThe reading of a pressure meter attached to a horizontal closed pipe is 3×105Nm−2. This reading falls to 1×105Nm−2 when the value is opened. What is the speed of water flowing in the pipe?
View SolutionTheThe velocity of flow of water in the main water supply pipe is 1.0ms−1. What is the velocity in the deliverty pipe if area of cross-section of the supply pipe is 16 times that of the delivery pipe?
View Solution

