Two rods A and B are of equal length. Each rod has the ends at temp T1 and T2 . What is the condition that will ensure equal rates of flow of heat through the rods A and B ?
To determine the condition that ensures equal rates of heat flow through two rods A and B, we can use the formula for heat conduction, which is given by Fourier's law of heat conduction. The rate of heat flow (Q/t) through a rod can be expressed as:
Qt=k⋅A⋅(T1−T2)L
where:
- Q is the amount of heat transferred,
- t is the time,
- k is the thermal conductivity of the material,
- A is the cross-sectional area of the rod,
- T1 and T2 are the temperatures at the ends of the rod,
- L is the length of the rod.
1. Identify the Variables:
For rods A and B, we have:
- Lengths: LA=LB
- Cross-sectional areas: AA and AB
- Thermal conductivities: kA and kB
- Temperature difference: ΔT=T1−T2 (assumed to be the same for both rods).
2. Set Up the Heat Flow Equations:
For rod A, the rate of heat flow is:
QAt=kA⋅AA⋅(T1−T2)LA
For rod B, the rate of heat flow is:
QBt=kB⋅AB⋅(T1−T2)LB
3. Equate the Heat Flow Rates:
To ensure equal rates of heat flow through both rods, we set the two equations equal to each other:
kA⋅AA⋅(T1−T2)LA=kB⋅AB⋅(T1−T2)LB
4. Simplify the Equation:
Since LA=LB and (T1−T2) is the same for both rods, we can cancel these terms:
kA⋅AA=kB⋅AB
5. Rearrange to Find the Condition:
Rearranging gives us:
AAAB=kBkA
Conclusion:
The condition that will ensure equal rates of flow of heat through rods A and B is:
AAAB=kBkA
- Q is the amount of heat transferred,
- t is the time,
- k is the thermal conductivity of the material,
- A is the cross-sectional area of the rod,
- T1 and T2 are the temperatures at the ends of the rod,
- L is the length of the rod.
For rods A and B, we have:
- Lengths: LA=LB
- Cross-sectional areas: AA and AB
- Thermal conductivities: kA and kB
- Temperature difference: ΔT=T1−T2 (assumed to be the same for both rods).
For rod A, the rate of heat flow is:
QAt=kA⋅AA⋅(T1−T2)LA
For rod B, the rate of heat flow is:
QBt=kB⋅AB⋅(T1−T2)LB
To ensure equal rates of heat flow through both rods, we set the two equations equal to each other:
kA⋅AA⋅(T1−T2)LA=kB⋅AB⋅(T1−T2)LB
Since LA=LB and (T1−T2) is the same for both rods, we can cancel these terms:
kA⋅AA=kB⋅AB
Rearranging gives us:
AAAB=kBkA
The condition that will ensure equal rates of flow of heat through rods A and B is:
AAAB=kBkA
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions
21 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - NCERT Questions
73 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Solved Examples
159 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
Two rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View SolutionNine identical conducting rods are arranged as shown in the figure. The ends A and B are maintained at temperatues T1 and T2. Calculate the ratio of rate of flow of heat across AD to that of EB in the given arrangement in steady state.
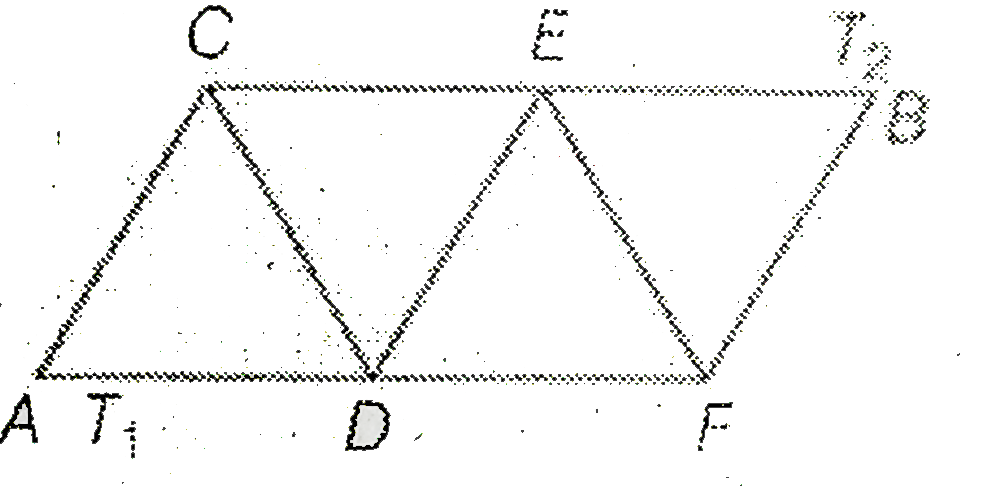
View Solution
Knowledge Check
Two rods A and B have lengths l1andl2. Each rod has its ends at temperature T1andT2 Radii fo cross section of the two rods are same. The condition for equal flow of heat through those two rods is (K1,K2 are thermal conductivities of two rods)
AK1I1=K2I2BK1I2=K2I1CK1=K2DI1=I2A metallic rod is continuously heated at its two ends, the flow of heat through the rod does not depend upon –
AThe area of cross section of the rodBThe mass of the rodCTimeDThe temperature gradientTwo rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
AA1A2=L1K2BA1A2=K2K1CA1A2=K1K2Dplaced in hot oil
Equal temperature difference exists between the ends of two metallic rods 1 and 2of equal length. Their thermal conduetivities are K1 and K2 and cross sectional areas are respectively A1 and A2. The condition for equal rate of heat transfer will be-
View SolutionIf the end of metal rod is heated then the rate of flow the heat does not depend on
View SolutionThe ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
View SolutionTwo rods of same length and areas of cross section A1 and A2 have their ends at same temperature. If K1 and K2 are their thermal conductivities, C1 and C2 their specific heats and ρ1 and ρ2 are their densities, then the condition that rate of flow of heat is same in both the rods is
View SolutionThe heat is flowing through two cylinderical rods of same material. The diameters of the rods are in the ratio 1:2 and their lengths are in the ratio 2:1. If the temperature difference between their ends is the same, the ratio of rates of flow of heat through them will be
View Solution
