The electrical resistance in ohms of a certain thermometer varies with temperature ac cording to the approximate law: R=R0[1+α(T−T0)]
The resistances is 101.6Ω at the triple-point of water 273.16K, and 165.5Ω at the normal melting point of lead (600.5K). What is the temperature when the resistance is 123.4Ω?
To solve the problem step by step, we will follow the given formula for resistance and the provided data points to find the temperature when the resistance is 123.4 ohms.
Step 1: Identify the known values
We have the following known values:
- Resistance at the triple point of water (R₀): 101.6 Ω at T₀ = 273.16 K
- Resistance at the normal melting point of lead (R₁): 165.5 Ω at T₁ = 600.5 K
- Resistance we want to find the temperature for (R): 123.4 Ω
Step 2: Use the resistance-temperature relationship
The relationship given is:
R=R0(1+α(T−T0))
Step 3: Set up equations for the known points
Using the known values, we can set up two equations:
1. For the triple point of water:
101.6=101.6(1+α(273.16−273.16))
This simplifies to:
1=1 (which is trivially true)
2. For the melting point of lead:
165.5=101.6(1+α(600.5−273.16))
Step 4: Solve for α
From the second equation:
165.5=101.6(1+α(327.34))
Dividing both sides by 101.6:
165.5101.6=1+α(327.34)
Calculating the left side:
1.628=1+α(327.34)
Subtracting 1 from both sides:
0.628=α(327.34)
Now, solving for α:
α=0.628327.34
Calculating α gives:
α≈0.00192K−1
Step 5: Set up the equation for the unknown resistance
Now we will use the resistance value of 123.4 Ω:
123.4=101.6(1+0.00192(T−273.16))
Step 6: Solve for T
Dividing both sides by 101.6:
123.4101.6=1+0.00192(T−273.16)
Calculating the left side:
1.214=1+0.00192(T−273.16)
Subtracting 1 from both sides:
0.214=0.00192(T−273.16)
Now, divide by 0.00192:
T−273.16=0.2140.00192
Calculating the right side gives:
T−273.16≈111.67
Adding 273.16 to both sides:
T≈384.83K
Final Answer
The temperature when the resistance is 123.4 Ω is approximately 384.83 K.
We have the following known values:
- Resistance at the triple point of water (R₀): 101.6 Ω at T₀ = 273.16 K
- Resistance at the normal melting point of lead (R₁): 165.5 Ω at T₁ = 600.5 K
- Resistance we want to find the temperature for (R): 123.4 Ω
The relationship given is:
R=R0(1+α(T−T0))
Using the known values, we can set up two equations:
1. For the triple point of water:
101.6=101.6(1+α(273.16−273.16))
This simplifies to:
1=1 (which is trivially true)
165.5=101.6(1+α(600.5−273.16))
From the second equation:
165.5=101.6(1+α(327.34))
Dividing both sides by 101.6:
165.5101.6=1+α(327.34)
Calculating the left side:
1.628=1+α(327.34)
Subtracting 1 from both sides:
0.628=α(327.34)
Now, solving for α:
α=0.628327.34
Calculating α gives:
α≈0.00192K−1
Now we will use the resistance value of 123.4 Ω:
123.4=101.6(1+0.00192(T−273.16))
Dividing both sides by 101.6:
123.4101.6=1+0.00192(T−273.16)
Calculating the left side:
1.214=1+0.00192(T−273.16)
Subtracting 1 from both sides:
0.214=0.00192(T−273.16)
Now, divide by 0.00192:
T−273.16=0.2140.00192
Calculating the right side gives:
T−273.16≈111.67
Adding 273.16 to both sides:
T≈384.83K
The temperature when the resistance is 123.4 Ω is approximately 384.83 K.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Higher Order thinking skells17videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Value Based Question5videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions21videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
Similar Questions
The resistance of the platinum resistance thermometer at the triple point of water is 15.00Ω and that when put inside the furnace is found to be 30.00Ω. What is the temperature of the furnace?
View SolutionThe resistance of a conductor at 20∘Cis6.3Ωandat100∘C it is 7.5Ω . Calculate the resistance of the conductor at 0∘C and its temperature coefficient of resistance .
View Solution
Knowledge Check
- Question 1 - Select One
The resistance t R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
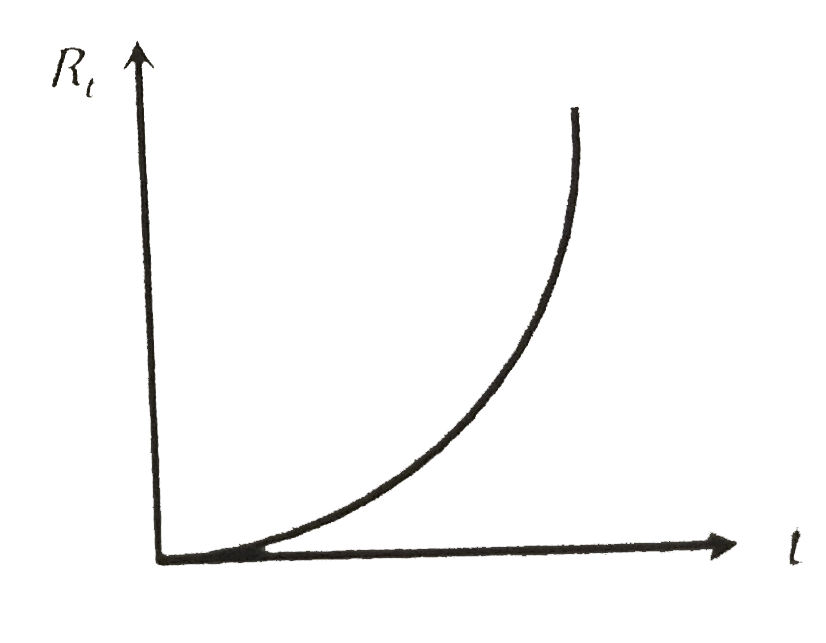 Aα and β are both negativeBα and β are both positiveCα is positive and β is negativeDα is negative and β are positive
Aα and β are both negativeBα and β are both positiveCα is positive and β is negativeDα is negative and β are positive - Question 2 - Select One
The temperature coefficient of resistance of wire is 0.001259∘C−1. If resistance is 1Ω at 300 K, then 2Ω will be at:
A1400 KB1100 KC1127 JD1154 K - Question 3 - Select One
Choose the most appropriate option.
The resistance R of a conductor varies with temperature t as shown in figure. If the variation is represented by Rt=R0(1+αt+βt2).
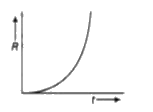
ThenAαandβ bothe negativeBα is positive and β is negativeCαandβ both are positiveDα is negative and β is negative
The resistance of a thin silver wire is 1.0 Ω at 20∘C. The wire is placed in liquid bath and its resistance rises to 1.2 Ω. What is the temperature of the bath ? (Here α=10−2/∘C)
View SolutionThe temperature coefficient of a resistance wire is 0.0012∘C−1. At 300 K, its resistance is 1Ω. At what temperature the resistance of the wire will be 2Ω ?
View SolutionA conducting wire has a resistance of 5Ωat0∘Cand5.6Ωat100∘C. When the wire is inserted in a hot bath with temperature T∘C , its resistance is 5.9Ω . What is the value of T ?
View SolutionA 100 volt voltmeter whose resistance is 20 kΩ is connected in series to a very high resistance R. When it is joined in a line of 110 volt, it reads 5 volt. What is the magnitude of resistance R ?
View SolutionThe temperature co-effcient of resistance of a wire is 0.00125∘C. At 500 K, its resistance is 1Ω. The resistance of the wire will be 2Ω at
View Solution

