A concrete sphere of radius $R$ has cavity of radius $r$ which is packed with sawdust. The specific gravities of concrete and sawdust are respectively $2.4 and 0.3$ for this sphere to float with its entire volume submerged under water. Ratio of mass of concrete to mass of swadust will be

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

Let R be the radius of the whole sphere. Let $ρ_{1}, ρ_{2}$ be the specific gravity of concrete and saw dust respectively. Ac cording to principle of floatation, weight of whole sphere = upthrust $\frac{4}{3} π (R^{3} - r^{3}) ρ_{1} + \frac{4}{3} π r^{3} ρ_{2} = \frac{4}{3} π R^{3} \times 1$
or $R^{3} ρ_{1} - r^{3} ρ_{1} + r^{3} ρ_{2} = R^{3}$
or $R^{3} (ρ_{1} - 1) = r^{3} (ρ_{1} - ρ_{2})$
or $\frac{R^{3}}{r^{3}} = \frac{(ρ_{1} - ρ_{2})}{(ρ_{1} - ρ_{1})}$
$or \frac{R^{3} - r^{3}}{r^{3}} = \frac{(ρ_{1} - ρ_{2}) - (ρ_{1} - 1)}{(ρ_{1} - 1)}$
or $\frac{(R^{3} - r^{3}) ρ_{1}}{r^{3} ρ_{2}} = (\frac{1 - ρ_{2}}{ρ_{1} - 1}) \times \frac{ρ_{1}}{ρ_{2}}$
$∴ \frac{Mass of concrete}{Mass of saw dust} = \frac{\frac{4}{3} π (R^{3} - r^{3}) ρ_{1}}{\frac{4}{3} π r^{3} ρ_{2}}$
$= \frac{(R^{3} - r^{3}) ρ_{1}}{r^{3} ρ_{2}} = \frac{(1 - ρ_{2}) ρ_{1}}{(ρ_{1} - 1) ρ_{2}}$
$= (\frac{1 - 0.3}{2.4 - 1}) \times \frac{2.4}{0.3} = 4$

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Inside a uniform sphere of mass M and radius R, a cavity of radius $R / 3$ , is made in the sphere as shown :

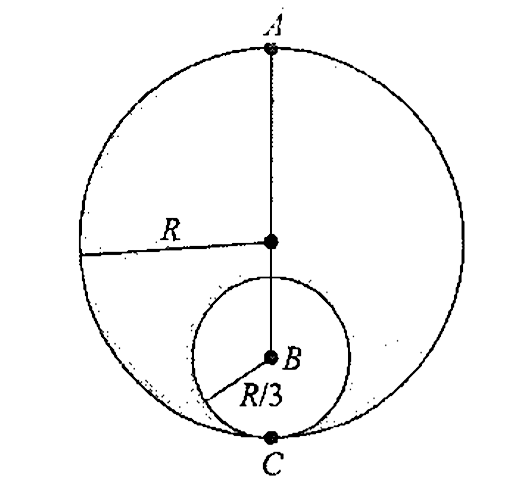AGravitational field inside the cavity is uniform
BGravitational field inside the cavity is non-uniform
CThe escape velocity of a particle projected from point A is $\sqrt{\frac{88 G M}{15 R}}$
DEscape velocity is defined for earth and particle system only
Question 2 - Select One
If the radius of a sphere is 2r , them its volume will be
A $\frac{4}{3} π r^{3}$
B $4 π r^{3}$
C $\frac{8 π r^{3}}{3}$
D $\frac{32}{3} π r^{3}$
Question 3 - Select One
A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
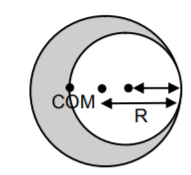A $(R^{2} + R + 1) (2 - R) = 1$
B $(R^{2} - R - 1) (2 - R) = 1$
C $(R^{2} - R + 1) (2 - R) = 1$
D $(R^{2} + R - 1) (2 - R) = 1$

PRADEEP-PROPERTIES OF BULK MATTER-Problmes for Practice

Home
Ask Doubt
Profile