Two tubes A and B of length 80 cm and 40 cm have radii 0.1 mm and 0.2 mm respectively are connected in series end to end. If a liquid passing through tow tubes is entering A at a pressure of 82 cm of mercury and leaving B at a pressure of 76 cm of mercury. Find the pressure at the junction of A and B.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:76.18 cm of Hg

Let Pj (in cm of Hg) be the pressure at the junction of A and B.
For of flow of liquid through tube A,
Q1=π(PA−Pj)r418ηl1=π(82−Pj)(0.01)48η×80
For tube B:l2=40cm,r2=0.02cm,
Pressure at which liquid leaves tube B,
PB=76 cm of Hg
Rate of flow of liquid through tube B
Q2=⎛⎝πPj0−PBr428ηl=π(Pj−76)(0.02)48η×40⎞⎠
Here,
∴π(82−Pj)×(0.01)48η×80=π(Pj−76)(0.02)48η×40
or (82−Pj)=(Pj−76)×32
On solving, Pj=76.18 cm of Hg

Updated on:21/07/2023
|
Class 11PHYSICSPROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The number of molecules in 1cm3 of an ideal gas at 0∘C and at a pressure of 10–5 mm of mercury is –

    A2.7×1011
    B3.5×1011
    C6.0×1023
    D6×1012

  • In the given figure, atmospheric pressure p0=1 atm and mercury column length is 9 cm. Pressure p of the gas enclosed in the tube is
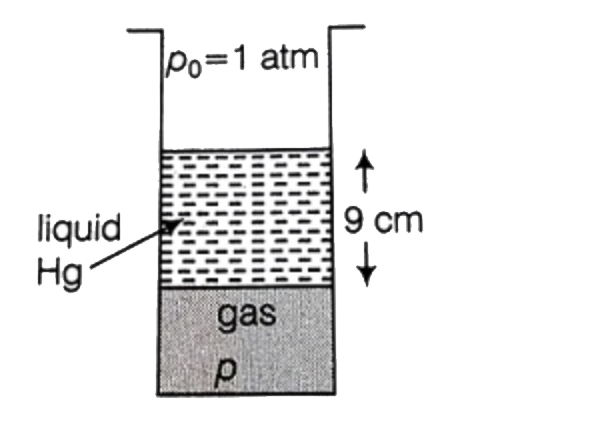    ocr_image

    APressure of 67 cm of Hg
    BPressure of 90 cm of Hg
    CPressure of 78 cm of Hg
    DPressure of 85 cm of Hg

  • Three capillaries of internal radii 2r, 3r and 4r, all of the same length, are joined end to end. A liquid passes through the combination and the pressure difference across this combination is 20.2 cm of mercury. The pressure differene across the capillary of internal radius 2r is

    A2cm of Hg
    B4cm of Hg
    C8cm of Hg
    D16cm of Hg