The opening near the bottom of the vessel shown in the figure has an area A. A disc is held against the opening keep the liquid from running out. Let F1 be the net forces on the disc applied by liquid and air in this case. Now the disc is moved away from the opening a short distance. The liquid comes out and strikes the disc in elastically. Let F2 be the force exerted by the liquid in this condition. The F1/F2 is

The correct Answer is:[1/2]
Let ρ the density of liquid. Then
F1=(δP)A=ρghA
In the second case, F2=rate of change of momentum
= mass of water striking per sec x velocity
=(Av×ρ)×v=Aρv2=Aρ(√2gh)2
=Aρ×2gh
∴F1F2=12
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-I
173 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Fill in the Blanks E
10 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
The opening near the bottom of the vessel shown has an area A. A disk is held against the opening to keep the liquid, from running out. It is given that net force on the disk applied by liquid and air in this case is F. Now the disc is moved away from the opening by a short distance. The liuid comes out and strikes the disk inelastically. What will be the initial force exerted by the liquid on the disk in this condition.

View SolutionFind the centre of mass of the disc shown in figure. . A square is removed from the disc as shown
View Solution
Knowledge Check
Some liquid is filled in a cylindrical vessel of radius R. Let F1 be the force applied by the liquid on the bottom of the cylinder. Now the same liquid is poured into a vessel of uniform square cross-section of side R. Let F2 be the force applied by the liquid on the bottom of this new vessel. (Neglect atmosphere pressure). Then
AF1=πF2BF1=F2πCF1=√πF2DF1=F2A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
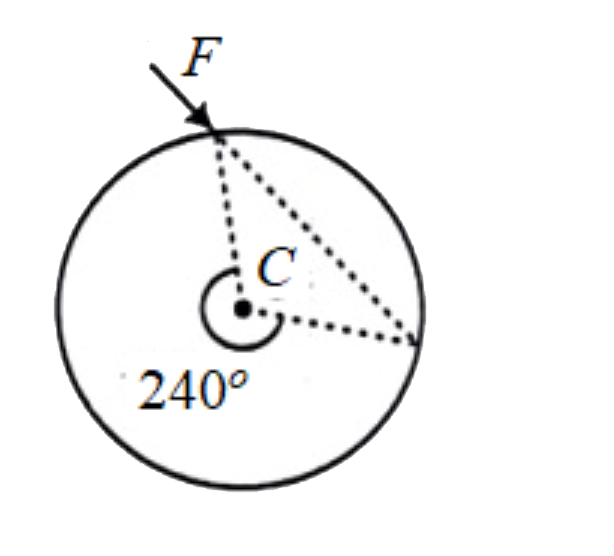 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRA liquid of density ρ comes out with a velocity v from a horizontal tube of area of cross-section A. The reaction force exerted by the liquid on the tube is F :
AF∝vBF∝v2CF∝ADF∝ρ
A disc is placed on the surface of pond filled with liquid of refractive index 53. A source of light is placed 4m below the surface of liquid. Calculate the minimum area of the disc so that light does not come out of liquid.
View SolutionA disc is placed on the ground. Friction coefficient is μ. What is the minimum force required to move the disc if it is applied at the topmost point?
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
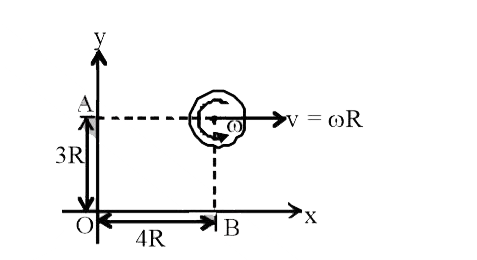
View SolutionPlace a coin on gramophone disc near its centre and set the disc into the rotation. As the speed of rotation increases, the coin will slide away from the centre of the disc. The motion of coin is due to
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View Solution
