An alumminium rod and steel wire of same length and cross-section are attached end to end. Then compound wire is hung fron a rigid support and load is suspended from the free end. Y for steel is (207) times of aluminium. The ratio of increase in length of steel wire to the aluminium wire is
20:3
10:7
7:20
1:7
The correct Answer is:C
Here, Ys=207Ya or YsYa=207
As Y=FLAΔL or ΔL=FLAY
ΔL∝1Y as both the wires are of same length.
ΔLsΔLa=YaYs=1(Ys/Ya)=120/7=720
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Integer Type Questions
12 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Asseration - Reason Type Question
18 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
A copper wire and a steel wire of the same length and same cross-section are joined end to end to form a composite wire. The composite wire is hung form a rigid support and a load is suspended form the other end. If the increses in length of the composite wire is 2.4mm. then the increases in lenghts of steel and copper wires are
View SolutionAn Aluminum and Copper wire of same cross sectional area but having lengths in the ratio 2:3 are joined end to end. This composite wire is hung form a rigid support and a load is suspended form the free end. If the increases in length of the composite wire is 2.1mm the increses in lenghts of Aluminimum and Copper wirs are
View Solution
Knowledge Check
An aluminum wire and a steel wire of the same length and cross-section are joined end to end. The compoiste wire is hung from a rigid support and a load is suspended from the free end. If the length of the composite wire is 2.7mm then the increases in the length of wire is (in mm)
(YAl=2×1011Nm2,YSteel=7×1011Nm−2)A1.7,1B1.3,4C1.5,1.2D2.1,0.6An aluminium wire and a steel wire of the same length and cross section are joined end to end. The composite wire is hung from a rigid support and the load is suspended at the free end. If YAL=7×1010N/m2 and Ysteel=7×1011N/m2, the ratio of elongation of aluminium and steel wires is
AeAeS=5BeAeS=8CeAeS=10DeAeS=2.5A copper wire and a steel wire of same length and same cross-section are joined end to end. The compositive wire is hung from a rigid support and a load is suspended form the free end. The increase in length of the compositive wire is 4 mm. The increase in copper wire will be
(Ycopper=1.2×1011N/m2,Ysteel=2×1011N/m2)A3 mmB1.5 mmC2 mmD2.5 mm
A mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
View SolutionA mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars,
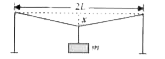
A mass m is suspended from the midpoint of the wire. Strain in the wire is
View SolutionA mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
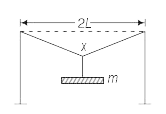
View SolutionA metal wire of length L1 and area of cross-section A is attached to a rigid support. Another metal wire of length L2 and of the same cross-sectional area is attached to free end of the first wire. A body of mass M is then suspended from the free end of the second wire. If Y1andY2 are the Young's moduli of the wires respectively, the effective force constant of the system of two wire is
View SolutionA steel wire 2m long is suspended from the ceiling. When a mass is hung from its lower end, the increase in length recorded is 1cm. Determine the strain in the wire.
View Solution
