A narrow uniform glass tube contains air enclosed by 15 cm long thread of mercury. When the tube is vertical with open end uppermost, the air column is 30 cm long. When the tube is inverted, the length of air column becomes 45 cm. Calculate the atmospheric pressure.
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the setup
- We have a glass tube with a mercury thread that is 15 cm long.
- When the tube is vertical, the air column is 30 cm long.
- When the tube is inverted, the air column becomes 45 cm long.
Step 2: Analyze the vertical position
In the vertical position:
- The height of the mercury column (h₁) is equal to the length of the mercury thread, which is 15 cm.
- The length of the air column (L₁) is 30 cm.
- The total height of the mercury column plus the air column gives us the atmospheric pressure.
Using the formula for pressure:
Patm=Pair+Pmercury
Where:
- Pair is the pressure due to the air column,
- Pmercury is the pressure due to the mercury column.
The pressure due to the air column can be given as:
Pair=ρair⋅g⋅L1
Where:
- ρair is the density of air,
- g is the acceleration due to gravity,
- L1=30cm=0.30m.
The pressure due to the mercury column is:
Pmercury=ρmercury⋅g⋅h1
Where:
- ρmercury is the density of mercury,
- h1=15cm=0.15m.
Step 3: Analyze the inverted position
In the inverted position:
- The length of the air column (L₂) is now 45 cm.
- The pressure due to the air column is given by:
Pair=ρair⋅g⋅L2
Where L2=45cm=0.45m.
Step 4: Set up the equations
From the vertical position, we can express the atmospheric pressure as:
Patm=ρair⋅g⋅L1+ρmercury⋅g⋅h1
From the inverted position, we can express the atmospheric pressure as:
Patm=ρair⋅g⋅L2+ρmercury⋅g⋅h1
Step 5: Equate the two expressions for atmospheric pressure
Since both expressions equal Patm, we can set them equal to each other:
ρair⋅g⋅L1+ρmercury⋅g⋅h1=ρair⋅g⋅L2+ρmercury⋅g⋅h1
Step 6: Simplify the equation
We can cancel out the ρmercury⋅g⋅h1 from both sides:
ρair⋅g⋅L1=ρair⋅g⋅L2
Step 7: Solve for atmospheric pressure
Rearranging gives:
ρair⋅g⋅(L2−L1)=0
This indicates that the difference in air column lengths is equal to the height of the mercury column:
L2−L1=hmercury
Step 8: Calculate atmospheric pressure
Using the known values:
- L1=0.30m
- L2=0.45m
- hmercury=0.15m
We can find the atmospheric pressure using the density of mercury (approximately 13,600kg/m3) and the acceleration due to gravity (g≈9.81m/s2):
Patm=ρmercury⋅g⋅hmercury
Calculating gives:
Patm=13600⋅9.81⋅0.15
Patm≈199.5kPa
Final Answer
The atmospheric pressure is approximately 199.5 kPa.
- We have a glass tube with a mercury thread that is 15 cm long.
- When the tube is vertical, the air column is 30 cm long.
- When the tube is inverted, the air column becomes 45 cm long.
In the vertical position:
- The height of the mercury column (h₁) is equal to the length of the mercury thread, which is 15 cm.
- The length of the air column (L₁) is 30 cm.
- The total height of the mercury column plus the air column gives us the atmospheric pressure.
Patm=Pair+Pmercury
Where:
- Pair is the pressure due to the air column,
- Pmercury is the pressure due to the mercury column.
Pair=ρair⋅g⋅L1
Where:
- ρair is the density of air,
- g is the acceleration due to gravity,
- L1=30cm=0.30m.
Pmercury=ρmercury⋅g⋅h1
Where:
- ρmercury is the density of mercury,
- h1=15cm=0.15m.
In the inverted position:
- The length of the air column (L₂) is now 45 cm.
- The pressure due to the air column is given by:
Pair=ρair⋅g⋅L2
Where L2=45cm=0.45m.
From the vertical position, we can express the atmospheric pressure as:
Patm=ρair⋅g⋅L1+ρmercury⋅g⋅h1
Patm=ρair⋅g⋅L2+ρmercury⋅g⋅h1
Since both expressions equal Patm, we can set them equal to each other:
ρair⋅g⋅L1+ρmercury⋅g⋅h1=ρair⋅g⋅L2+ρmercury⋅g⋅h1
We can cancel out the ρmercury⋅g⋅h1 from both sides:
ρair⋅g⋅L1=ρair⋅g⋅L2
Rearranging gives:
ρair⋅g⋅(L2−L1)=0
L2−L1=hmercury
Using the known values:
- L1=0.30m
- L2=0.45m
- hmercury=0.15m
Patm=ρmercury⋅g⋅hmercury
Patm=13600⋅9.81⋅0.15
Patm≈199.5kPa
The atmospheric pressure is approximately 199.5 kPa.
Topper's Solved these Questions
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBook:PRADEEPChapter:BEHAVIOUR OF PERFECT GAS & KINETIC THEORYExercise:Conceptual Problems
Explore 23 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBook:PRADEEPChapter:BEHAVIOUR OF PERFECT GAS & KINETIC THEORYExercise:Very short Answer questions
Explore 35 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBook:PRADEEPChapter:BEHAVIOUR OF PERFECT GAS & KINETIC THEORYExercise:Curiosity Question
Explore 2 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
Similar Questions
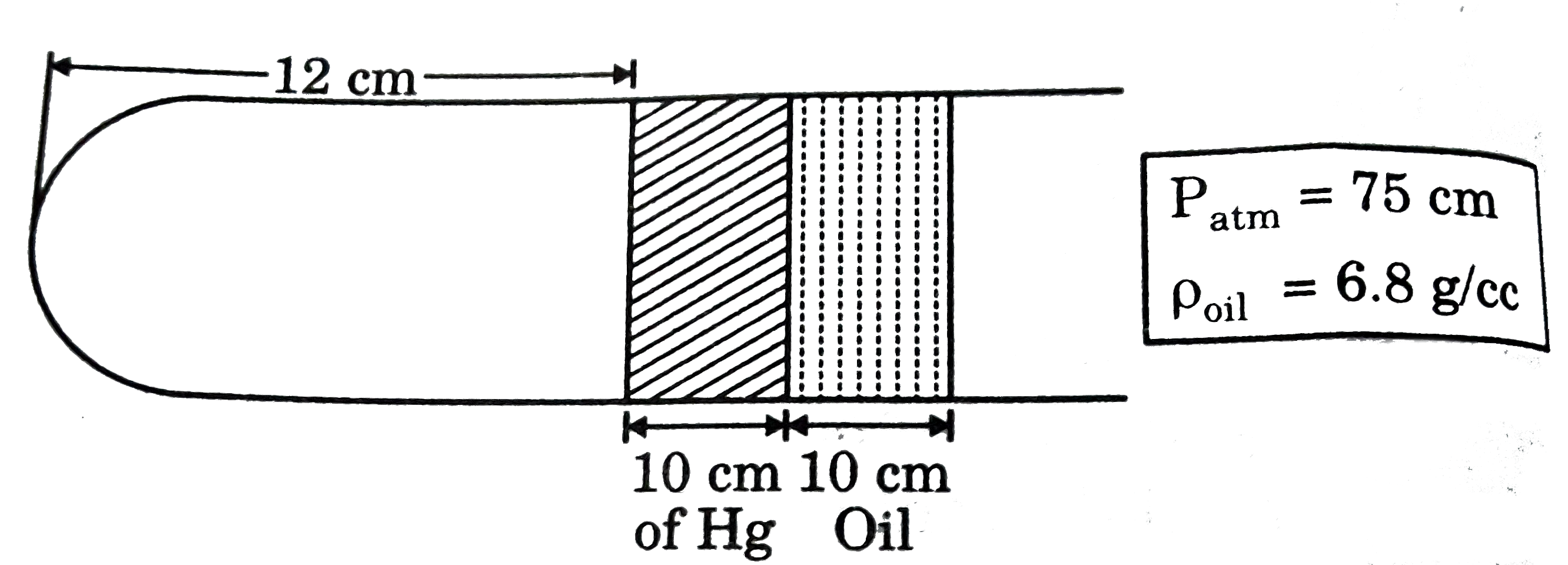
If above tube is held vertical with open end upward then find the length of air column (in cm).
View SolutionAn air column closed in a tube sealed at one end by a Hg column having height h. When the tube is placed with open end down, the height of the air column Iis l1. If the tube is turned so that its open end is at the top, the height of the air column is l2. What is the atmospheric pressure (P0).
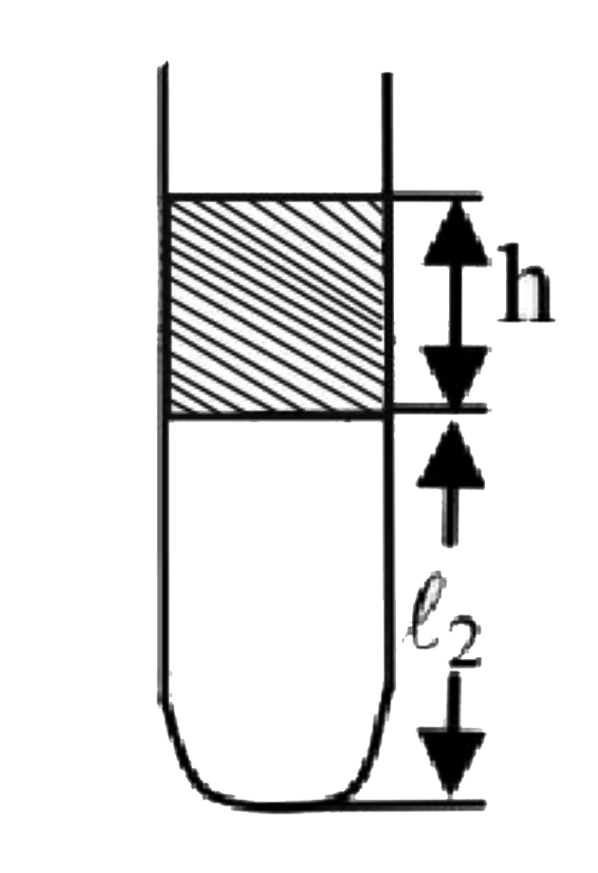
View Solution
Knowledge Check
When an air column in a tube open at both the ends is set into vibration with
AOdd harmonics are presentBSome harmonics are presentCAll harmonic are presentDEven harmonics are presentAn open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)A(a) 16cmB(b) 22cmC(c) 38cmD(d) 6cm
In given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

View SolutionA uniform tube closed at one end, contains a pallet of mercury 4 cm long. When the tube is kept vertically with closed end upwards, the length of air column between closed end and mercury pallet is 10 cm. the tube is inverted so that open end becomes upwards. find the length of trapped air column (in cm) trapped. take atmospheric pressure 76 cm of Hg.
View SolutionA uniform tube closed at aone end, contains a pellet of mercury 10cm long. When the tube is lept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.
View Solution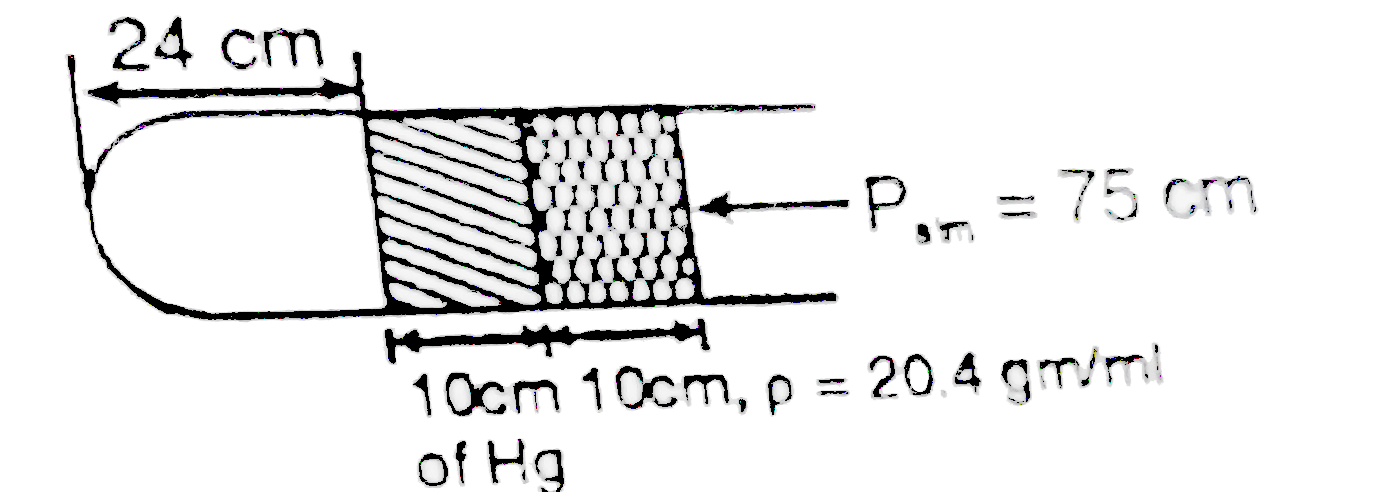
If above tube is placed vertically with the open and upward then find the length of the air column.
View SolutionA Quill's tube of one metre is taken. A certain amount of ideal gas is trapped in it by a 20 cm length of Hg column. When the tube is held vertical with open end upwards, the length of the gas column is 50 cm. Find the pressure and length of the trapped gas, when the Quill's tube is kept in slanting position making 45∘ with the vertical open and upwards. (Take atmospheric pressure as 76 cm of Hg and √2=1.414).
View SolutionA narrow uniform glass tube 80 cm long and open at both ends is half immersed in mercurry. Then the top of the tube is closed and it is taken out of mercury. A column of mercury 22 cm long then remains in the tube. What is the atmospheric pressure?
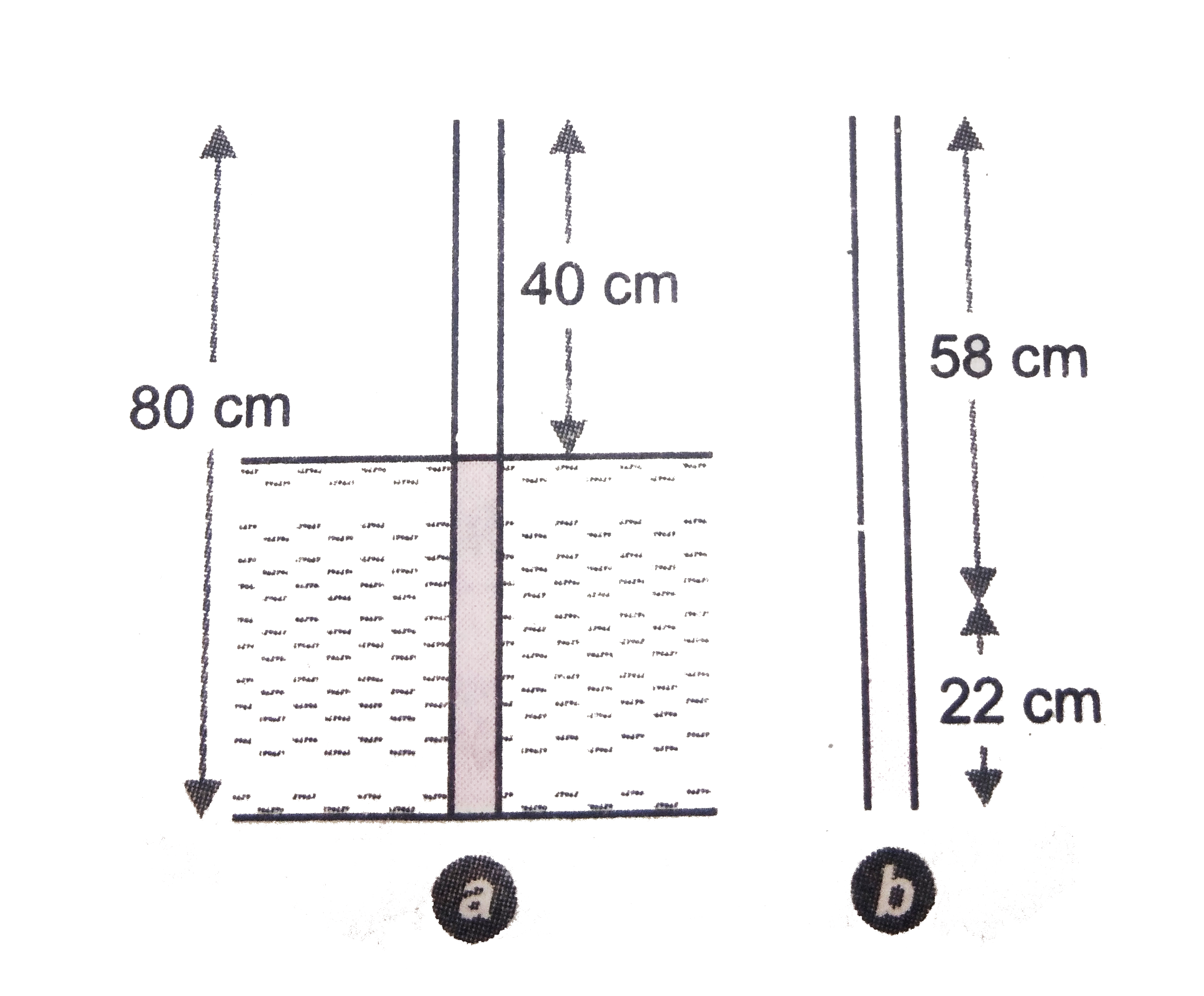
View Solution