A container of fixed volume has a mixture of a one mole of hydrogen and one mole of helium in equilibrium at temperature T. Assuming the gasses are ideal, the correct statement (s) is (are)
The average energy per mole of the gas mixture is 2 RT
The ratio of speed of sound in the gas mixture to that in helium gas is
The ratio of the rms speed of helium atoms to that of hydrogen molecules is
The ratio of the rms speed of helium atoms to that of hydrogen molecule is
The correct Answer is:A, B, D
Energy of 1 mole of and 1 mole of He
Energy per mole of mixture =
Velocity of sound in medium
or, .
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Multiple choice questions-III12videos
BEHAVIOUR OF PERFECT GAS & KINETIC THEORY
- BOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Integer type questions9videos
BEHAVIOUR OF PERFECT GAS & KINETIC THEORY
- BOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Multiple choice questions-I59videos
BEHAVIOUR OF PERFECT GAS & KINETIC THEORY
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
Similar Questions
A vessel of volume V contains n1 moles of oxygen and n2 moles of carbon dioxide at temperature T. Assuming the gases to be ideal, find,
(a) the pressure of the mixture,
(b) the mean molar mass of the mixture.View SolutionOne mole of oxygen is mixed withone mole of helium. What is γ of the mixture?
View Solution
Knowledge Check
- Question 1 - Select One or More
Two mole of Hydrogen and three mole of Helium are mixed at room temperature and at atmospheric pressure Pa and the mixture occupies a volume V.
ACV of mixture is 2RBCP of mixture is 2.9RCγ of mixture is nearly 1.53DIf the mixture is expanded adiabatically to 2V final pressure is Pa1.42 - Question 2 - Select One
A vessel of volume 20L contains a mixture o hydrogen and helium at temperature of 27∘C and pressure 2.0atm The mass of the mixture is 5g. Assuming the gases to be ideal, the ratio of the mass of hydrogen to heat of helium in the given mixture will be
A1:2B2:3C2:1D2:5 - Question 3 - Select One
A mixture of ideal gases has 2 moles of He, 4 moles of oxygen and 1 mole of ozone at absolute temperature T. The internal energy of mixture is
A13 RTB11 RTC16 RTD14 RT
The speed of sound in hydrogen gas at certain temperature is v ms Find the speed of sound in a gaseous mixture containing 2 moles of oxygen and 1 mole of hydrogen gas, at the same temperature. Assume the gases do no react at the ordinary temperature.
View SolutionA gas mixture consists of 3 moles of oxygen and 5 moles of argon at temperature T . Assuming the gases to be ideal and the oxygen bond to be rigid, the total internal energy ( in units of RT ) of the mixture is :
View SolutionA cylindrical container of volume 4.0×10−3m3 contains one mole of hydrogen and two moles of carbon dioxide. Assume the temperature of the mixture is 400 K. The pressure of the mixture of gases is :
[Take gas constant as 8.3Jmol−1K−1]View SolutionOne mole of a monatomic ideal gas goes through a thermodynamic cycle, as shown in the volume versus temperature diagram. The correct statement(s) is(are) :
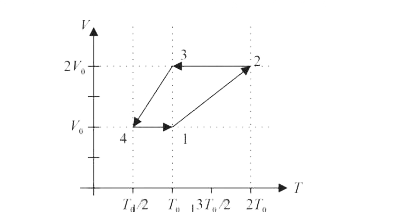 View Solution
View SolutionA vessel of volume 20L contains a mixture o hydrogen and helium at temperature of 27∘C and pressure 2.0atm The mass of the mixture is 5g. Assuming the gases to be ideal, the ratio of the mass of hydrogen to heat of helium in the given mixture will be
View Solution

