A point mass is subjected to two simultaneous sinusoidal displacements in x−direction,x1(t)=Asin(ω)tandx2(t)=Asin((ωt+2π3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mas to a complete rest. The values of (B) and (phi) are.
√2A,3π4
A,4π3
√3A,5π6
A,π3
The correct Answer is:B
Given, x1=Asinωt,x2=Asin(ωt+2π3)
∴x1+x2=Asinωt+Asin(ωt+2π3)
=Asinωt+A[sinωtcos(2π3)+cosωtsin(2π3)]
=Asinωt+A[sinωt×(−12)+cosωt×(√32)]
=A[12sinωt+(√32)cosωt]
=A[cos(π3)sinωt+sin(π3)cosωt]
=A sin(ωt+π3)
As per question, x1+x2+x3=0
∴x3=−(x91)+x2)=−Asin(ωt+4π3)
=Asin[ωt+π3+π]=Asin(ωt+4π3)
or B sin(ωt+ϕ)=Asin(ωt+4π3)
∴B=A,ϕ=4π3
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - integer type question8videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Assertion-Reason Type Questions23videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-II14videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
A point mass is subjected to two simultaneous sinusoidal displacement in x -direction, x1(t)=Asinωt and x2(t)=Asin(ωt+π2). Adding a third sinusoidal displacement x3t=Bsin(ωt+ϕ) brings the mass to a complete rest. The value of ϕ is nπ4. Then n is.
View SolutionIn y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
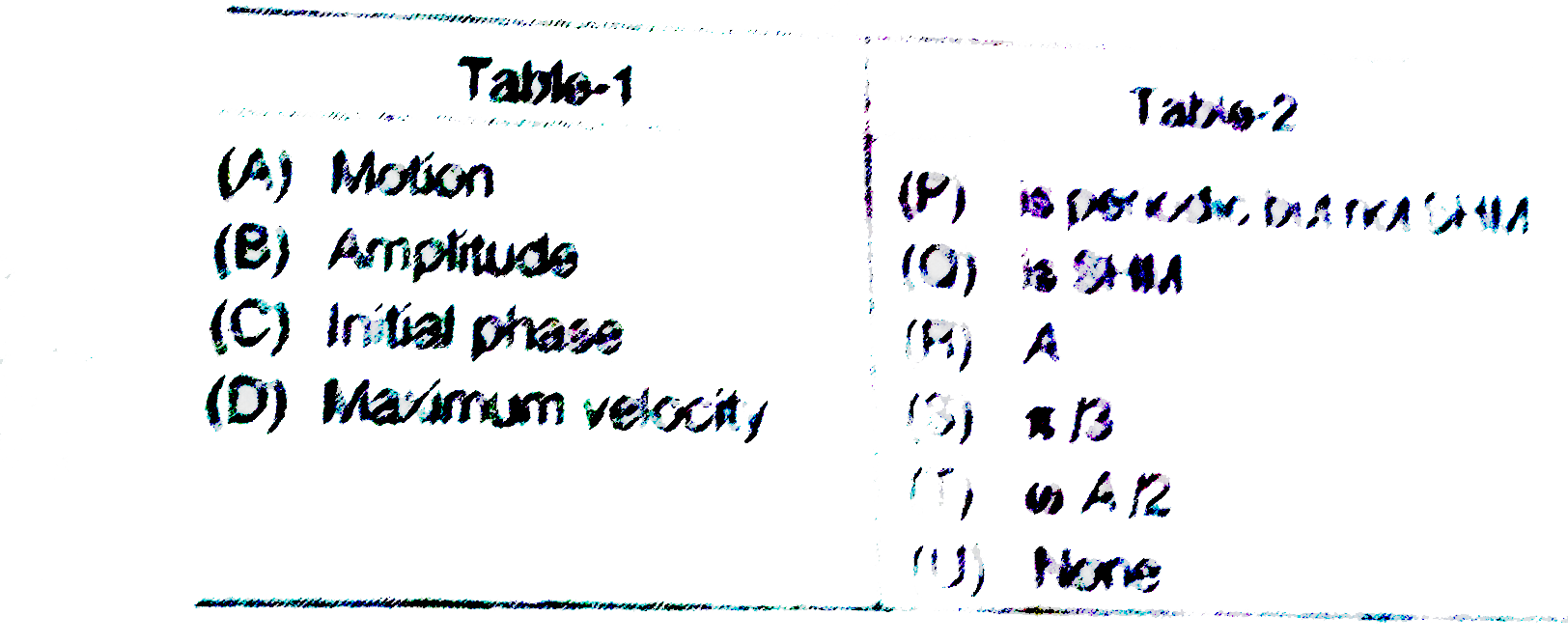 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A point mass is subjected to two simultaneous sinusoidal displacement in x−direction, x1(t)=Asinωt and x2(t)=Asin(ω+2π3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mass to complete rest. The value of B and ϕ are
A√2A,3π4BA,4π3C√3A,5π6DA,π3 - Question 2 - Select One
A point mass is subjected to two simultaneous sinusoidal displacement in x-direction, x1(t)=Asinωt and x2(t)=Asin(ωt+2π/3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mass to a complete rest. The values of B and ϕ are :
A√2A,3π4BA,4π3C√3A,5π6DA,π3 - Question 3 - Select One
The displacements of two interfering light waves are y1=2sinωt and y2=5sin(ωt+π3) the resultant amptitude is
A39cmB√39cmC7cmD√29cm
Find the displacement equation of the simple harmonic motion obtained by combining the motion.
x1=2sinωt, x2=4sin(ωt+π6) and x3=6sin(ωt+π3)View SolutionA partical is subjucted to two simple harmonic motions
x1=A1sinωt
and x2=A2sin(ωt+π/3)
Find(a) the displacement att=0, (b) the maximum speed of the partical and ( c) the maximum acceleration of the partical.View SolutionThe ratio of amplitudes of following SHM is x1=Asinωtandx2=Asinωt+Acosωt
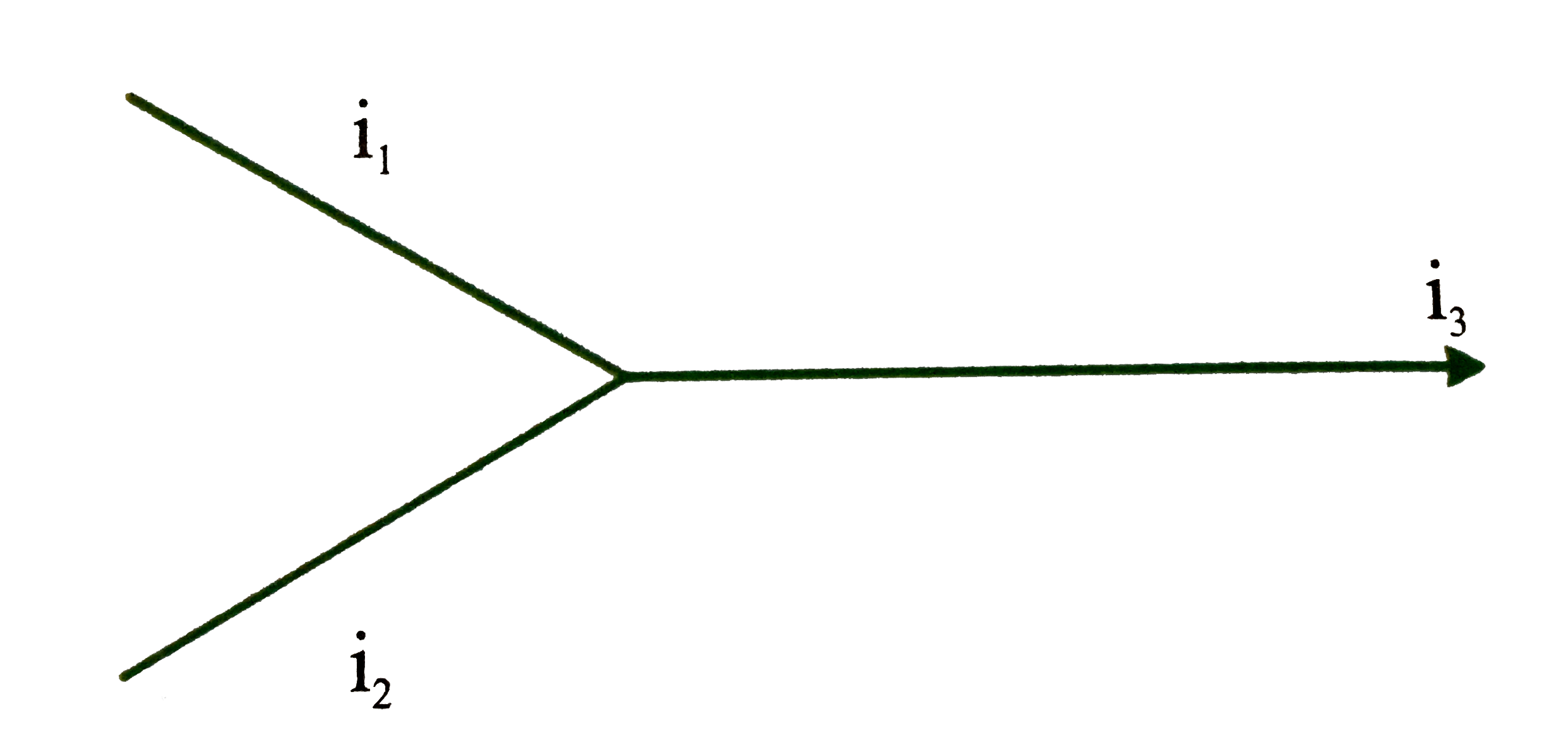
View SolutionIf i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
 View Solution
View SolutionThe equations of two SH M's are
X1=4sin(ωt+π/2).X2=3sin(ωt+π)View Solution

