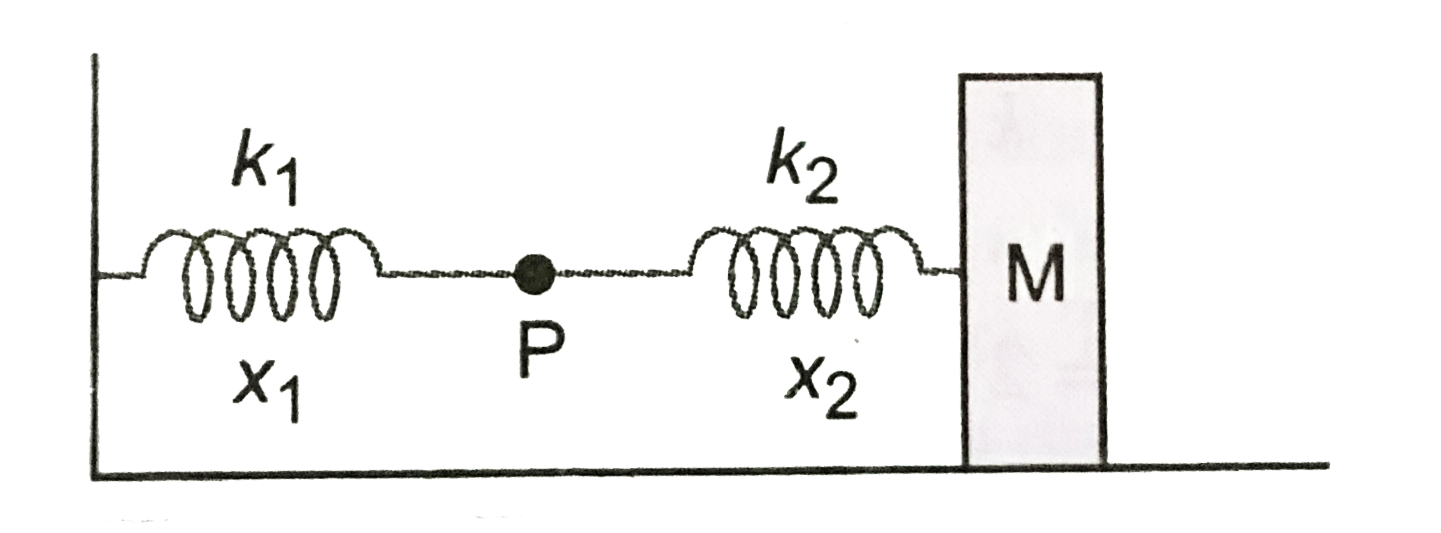
The mass (M) shown in the figure oscillates in simple harmonic motion with amplitude of the point (P) is.
 .
.
k1Ak2
k2Ak1
k1Ak1+k2
k2Ak1+k2
The correct Answer is:D
Refer to figure, Here the two springs are in series. Let the mass M be pulled through small distance A towards right hand side. Due to it, let x1 and x2 be the extension in two springs.
Here, the tnesion or the force is same for both the springs. So k1x1=k2x2 or x2=k1x1/k2.
Total extension, A=x1+x2
=x1+k1x1k2=x1(k2+k1k2)
∴ Amplitude of point P= extension of spring k1
=x1=k2Ak1+k2
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - integer type question8videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Assertion-Reason Type Questions23videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-II14videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
The figure shows a mass M attached to a series arrangement of two springs of spring constants k1andk2 where k2=2k1. If the mass M oscillates in simple harmonic motion with amplitude A, the amplitude of the point O is αAβ. Find β−α.
 View Solution
View SolutionA ball is rolling without slipping in a spherical shallow bowl (radius R) as shown in the figure and is executing simple harmonic motion. If the radius of the ball is doubled, the period of oscillation
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The maximum speed of junction P is V0. Assume springs are massless. Select the correct option/s
 AAmplitude of potential energy is springs S1 and S2 is respectivley 19kA2 and kA2BAmplitude of potential energy is S1 and S2 is respectively 29kA2 and 19kA2CV0=A√8k27MDV0=A√8k81M
AAmplitude of potential energy is springs S1 and S2 is respectivley 19kA2 and kA2BAmplitude of potential energy is S1 and S2 is respectively 29kA2 and 19kA2CV0=A√8k27MDV0=A√8k81M - Question 2 - Select One
The mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
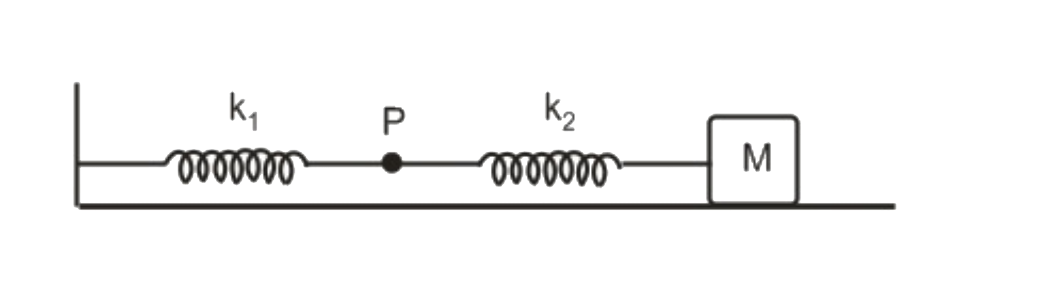 Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1
Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1 - Question 3 - Select One
The mass M shown in the figure oscillates in simple harmnonic motion and amplitude A. The amplitude of the point P is
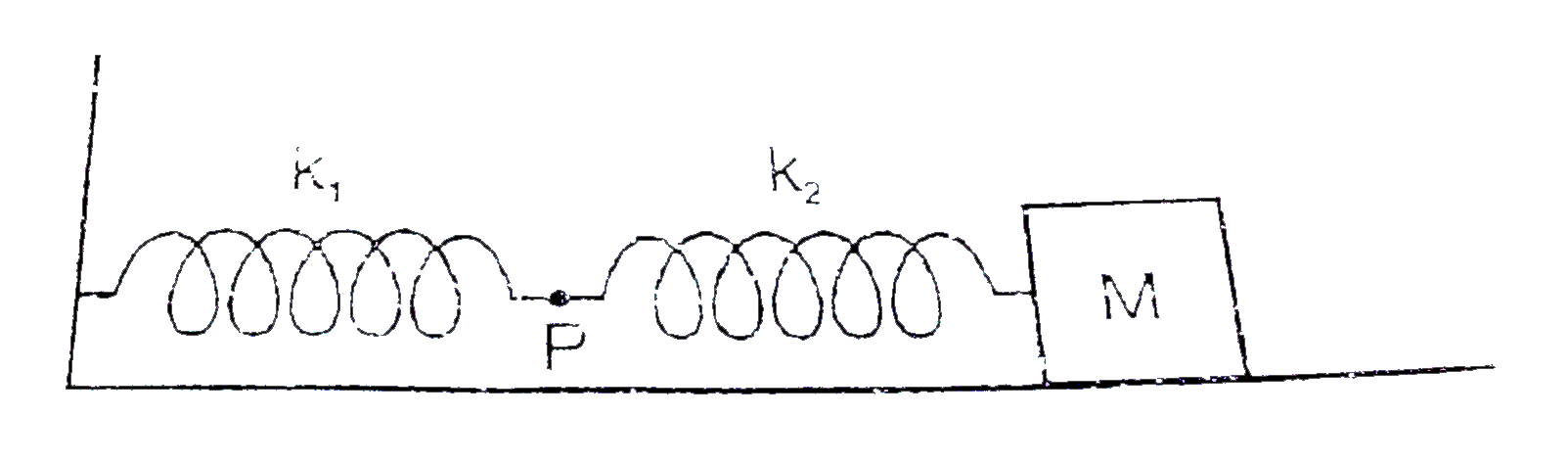 Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2
Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2
A system is oscillating with undamped simple harmonic motion. Then the
View SolutionA mass m oscillates with simple harmonic motion with frequency f=ω2πand amlitude A on a spring with constant K. therefore
View SolutionThe total work done by the restoring force in simple harmonic motion of amplitude A and angular velocity ω in one oscillation is
View SolutionThe maximum velocity a particle, executing simple harmonic motion with an amplitude 7 mm, 4.4 m//s. The period of oscillation is.
View SolutionA particle of mass m executes simple harmonic motion with amplitude a and frequency v. The average kinetic energy during its motion from the position of equilibrium to the ends is
View Solution

