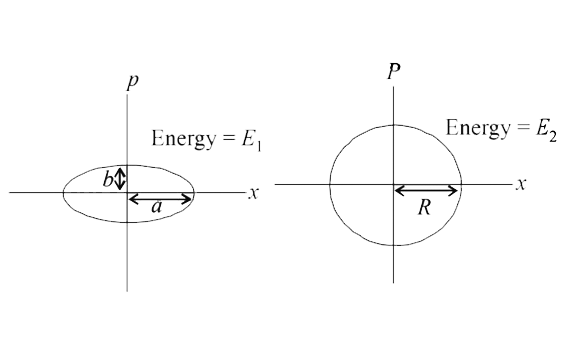
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies (omega_1) and (omega_2) and have total energies (E_1 and E_2), respectively. The variations of their momenta (p) with positions (x) are shown (s) is (are).

A

$E_{1} ω_{1} = E_{2} ω_{2}$

B

$\frac{ω_{2}}{ω_{1}} = n^{2}$

C

$ω_{1} ω_{2} = n^{2}$

D

$\frac{E_{1}}{ω_{1}} = \frac{E_{2}}{ω_{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, D

Refer of figure,
amplitude $A = a$
$p_{max} = b$ or $m υ_{max} = b$
or $m a ω_{1} = b$ ...(i)
$E_{1} = \frac{1}{2} m a^{2} ω_{1}^{2}$ ...(ii)
Refer to figure
$p_{max} = R,$ amplitude $A = R$
$m υ_{max}_(2)) = R$ or $m R ω_{2} = R$ or $m ω_{2} = 1$ ...(iii)
$E_{2} = \frac{1}{2} m R^{2} ω_{2}^{2}$ ...(iv)
From (ii) and (iv),
$\frac{E_{1}}{E_{2}} = \frac{a^{2} ω_{1}^{2}}{R^{2} ω_{2}^{2}} = \frac{n^{2} ω_{1}^{2}}{ω_{2}^{2}}$ ...(v)
$[∴ \frac{a}{R} = n]$
From (i) and (iii)
$\frac{a ω_{1}}{ω_{2}} = \frac{b}{2}$ or $\frac{ω_{1}}{ω_{2}} = \frac{b}{a} = \frac{1}{n^{2}}$ ..(vi)
or $\frac{ω_{2}}{ω_{1}} = n^{2}$ $[$ options (b) is true $]$
Putting the above value in (v) , we get
$\frac{E_{1}}{E_{2}} = \frac{ω_{2}}{ω_{1}} \times \frac{ω_{1}^{2}}{ω_{2}^{2}} = \frac{ω_{1}}{ω_{2}}$ or $\frac{E_{1}}{ω_{1}} = \frac{E_{2}}{ω_{2}}$
Hence, option (d) is true.

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies $ω_{1}$ and $ω_{2}$ and have total energies $E_{1}$ and $E_{2}$ repsectively. The variations of their momenta $p$ with positions $x$ are shown in figures. If $\frac{a}{b} = n^{2}$ and $\frac{a}{R} = n$ , then the correc t equation(s) is (are) :

A $E_{1} ω_{1} = E_{2} ω_{2}$
B $\frac{ω_{2}}{ω_{1}} = n^{2}$
C $ω_{1} ω_{2} = n^{2}$
D $\frac{E_{1}}{ω_{1}} = \frac{E_{2}}{ω_{2}}$
Question 2 - Select One
Two bodies of different masses $m_{1}$ and $m_{2}$ have equal momenta. Their kinetic energies $E_{1}$ and $E_{2}$ are in the ratio
A $\sqrt{m_{1}} : \sqrt{m_{2}}$
B $m_{1} : m_{2}$
C $m_{2} : m_{1}$
D $m_{1}^{2} : m_{2}^{2}$
Question 3 - Select One
For a linear harmonic oscillator, its potential energy, kinetic energy and total energy given by $E_{P}, K_{K} and E_{T}$ respectively. Its maximum acceleration is given by
A $\sqrt{\frac{2 E_{P}}{m}}$
B $\sqrt{\frac{2 E_{K}}{m}}$
C $\sqrt{\frac{2 E_{T}}{m A}}$
D $\frac{2 E_{T}}{m A}$

PRADEEP-OSCILLATIONS AND WAVES-JEE mains adv..(multiple choice quection)

Home
Ask Doubt
Profile