What happens to focal length of a convex lens when it is immersed in water ?
To determine what happens to the focal length of a convex lens when it is immersed in water, we can follow these steps:
Step 1: Understand the Lens Formula
The lens formula is given by:
1f=(n−1)(1r1−1r2)
where:
- f is the focal length of the lens,
- n is the refractive index of the lens material,
- r1 and r2 are the radii of curvature of the lens surfaces.
Step 2: Identify the Refractive Indices
When the lens is in air, the refractive index of air is approximately nair=1. If the lens has a refractive index n, then the effective refractive index μ when the lens is in air is:
μair=n−nair=n−1
When the lens is immersed in water, the refractive index of water is approximately nwater≈1.33. Thus, the effective refractive index μ when the lens is in water becomes:
μwater=n−nwater=n−1.33
Step 3: Compare the Effective Refractive Indices
Since the refractive index of the lens n is greater than that of water nwater, we can see that:
μwater<μair
This means that when the lens is in water, the value of μ decreases.
Step 4: Analyze the Effect on Focal Length
From the lens formula, we can see that the focal length f is inversely proportional to μ:
f∝1μ
Since μ decreases when the lens is immersed in water, the focal length f must increase.
Conclusion
When a convex lens is immersed in water, its focal length increases.
---
The lens formula is given by:
1f=(n−1)(1r1−1r2)
where:
- f is the focal length of the lens,
- n is the refractive index of the lens material,
- r1 and r2 are the radii of curvature of the lens surfaces.
When the lens is in air, the refractive index of air is approximately nair=1. If the lens has a refractive index n, then the effective refractive index μ when the lens is in air is:
μair=n−nair=n−1
μwater=n−nwater=n−1.33
Since the refractive index of the lens n is greater than that of water nwater, we can see that:
μwater<μair
This means that when the lens is in water, the value of μ decreases.
From the lens formula, we can see that the focal length f is inversely proportional to μ:
f∝1μ
Since μ decreases when the lens is immersed in water, the focal length f must increase.
When a convex lens is immersed in water, its focal length increases.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Conceptual problem(c)8videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Conceptual problem(d)14videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Solved Example(d)32videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions7videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions20videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A convex glass lens (μg=1.5) has a focal length of 8 cm when placed in air. What is the focal length of the lens when it is immersed in water ?
(μω=43)A32 cmB6 cmC16 cmD30 cm - Question 2 - Select One
Focal length of a convex lens is maximum for
Ablue lightByellow lightCgreen lightDred light - Question 3 - Select One
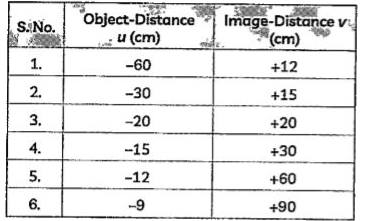
The focal length of the convex lens isA+10 cmB+20cmC−10cmD−20cm
The focal length of a convex lens is 25 cm. What is its power?
View SolutionFocal length of convex lens will miximum for
View SolutionFocal length of a convex lens will be maximum for
View SolutionFocal length of a convex lens will be maximum for
View Solution______ has shorter focal length convex lens
View Solution

