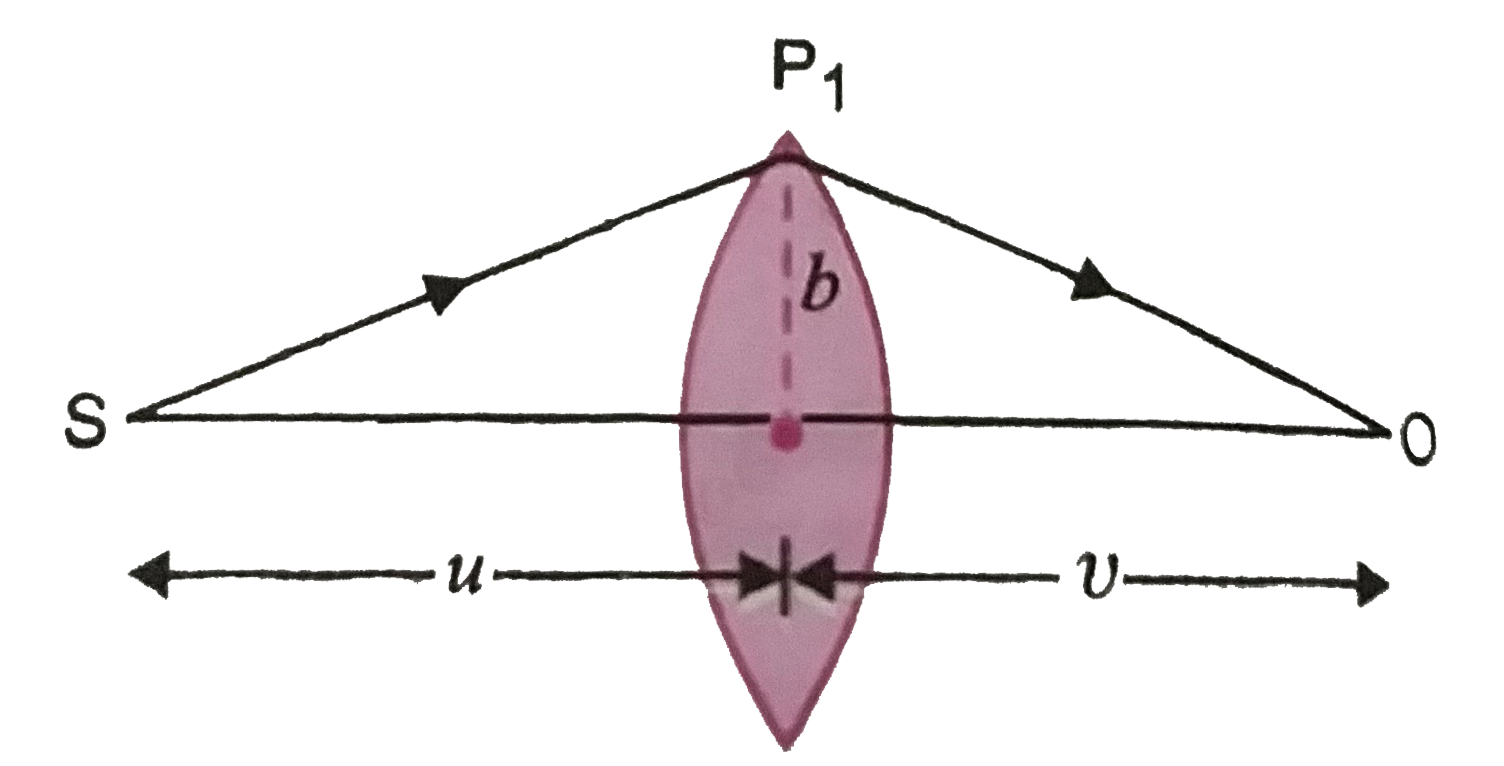
(i) Consider a thin lens placed between a source (S) and an observer (O), Fig. Let the thickness of the lens vary as w(b)=w0−b2∝, where b is the vertical distance from the pole. w0 is a constant. Using Fermat's principle, i.e., the time of transit for a ray between the source and observer is an exptremum, find the condition that al paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
(ii) A gravitational lens may be assumed to have a varying width of the form
w(b)=k1In(k2b)bmin<b<bmaxw(b)=k1In(k2bmin)b<bmin
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius β=√(n−1)k1uvu+v.
 .
.
Time required by ligth to travel in air from S→P1 is
t1=SP1c=√u2+b2c
=uc[1+12b2u2], assuming b<<u
Similarly, time required by light to travel in air from P1→O,=vc(1+12b2v2)
Now, thickness of lens varies as w(b)=w0−b2∝...(i)
∴ Time required to travel through the lens is t3=w(b)c/n−w(b)c=(n−1)w(b)c
Here, n is refractive index of the material of the lens.
Thus, the total time of travel from S→O is
t=t1+t2+t3=uc(1+b22u2)+vc(1+b22v2)+(n−1)w(b)c
t=1c[u+v+12b2(1u+1v)+(n−1)w(b)]
Let us put 1u+1v=1D ...(ii)
t=1c[u+v+b22D+(n−1)(w0−b2∝)]...(iii)
According to Fermat's principle, t = extremum. Therefore dtdb=0
From (iii), dtdb=bcD−2(n−1)bc∝=0 or ∝=2(n−1)D ...(iv)
Hence, a convergent lens is formed if ∝=2(n−1)D. This is independent of b. Hence, all paraxial rays from S will converge O.
From (ii), 1u+1v=1D. Therefore, focal length of lens =D
(ii) Now, for a gravitational lens, w(b)=k1loge(k2b),bmin<b<bmax
w(b)=k1loge(k2bmin),b<bmin
Proceeding as in the above case, from eqn. (iii)
t=12[u+v+12b2D+(n−1)k1loge(k2b)]
dtdb=0=bD−(n−1)k1b
∴b2=(n−1)k1D
b=√(n−1)k1D
Hence, all rays passing through the lens at a height b shall from the image.
The paths of rays would make an angle
β=bv=√(n−1)k1D√v2=√(n−1)k1uvv2(u+v) (as1d=1u+1v)
β=√(n−1)k1u/v(u+v)
Hence, the observer will see an image of a point object as a ring about the centre of the lens with with an angular radius β.
 .
.
Topper's Solved these Questions
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - (NCERT)Exercise With Solution
38 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Higher Thinking Order
5 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Long Answer (d)
6 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
Similar Questions

An object and the image obtained from the lens are as given above.
If the distance between the object and the image is 36 cm and the magnification is -2, find the focal length of the lens and draw the ray diagram to show the position of the lens.
View SolutionA source of light and screen are separated by a distance of 50 cm. A sharp image of the source is produced by lens when placed at two positions between the source and the screen. If the distance of separations of the lens between the two positions is 20 cm, find the focal length of the lens.
View Solution
Knowledge Check
Find the wrong statement from the following:
The relative speed between a source of sound and the observer is zero but the wind is blowing with a velocity Vw from the source to the obsever. In this caseAthere is no change in the frequency of the sound heardBthe velocity of sound is increased from V+VwCthe wavelength of sound heard is decreasedDthe wavelength of sound heard is increasedIf the distance between the observer and source decresase with time, then it show that
Aappartment frequency will be less than actual frequencyBappartment frequency will be greater than actual frequencyCappartment frequency will be equal to the actual frequencyDapparent frequencies cannot be noticedA screen is placed a distance 40 cm away from an illuminated object. A converging lens is palced between the source and the screen and it is attempted to form the image of the source on the screen. If no position could be found, the focal length of the lens
Amust be less than 10 cmBmust be greater than 20 cmCmust not be greater than 20 cmDmust not be less then 10 cm
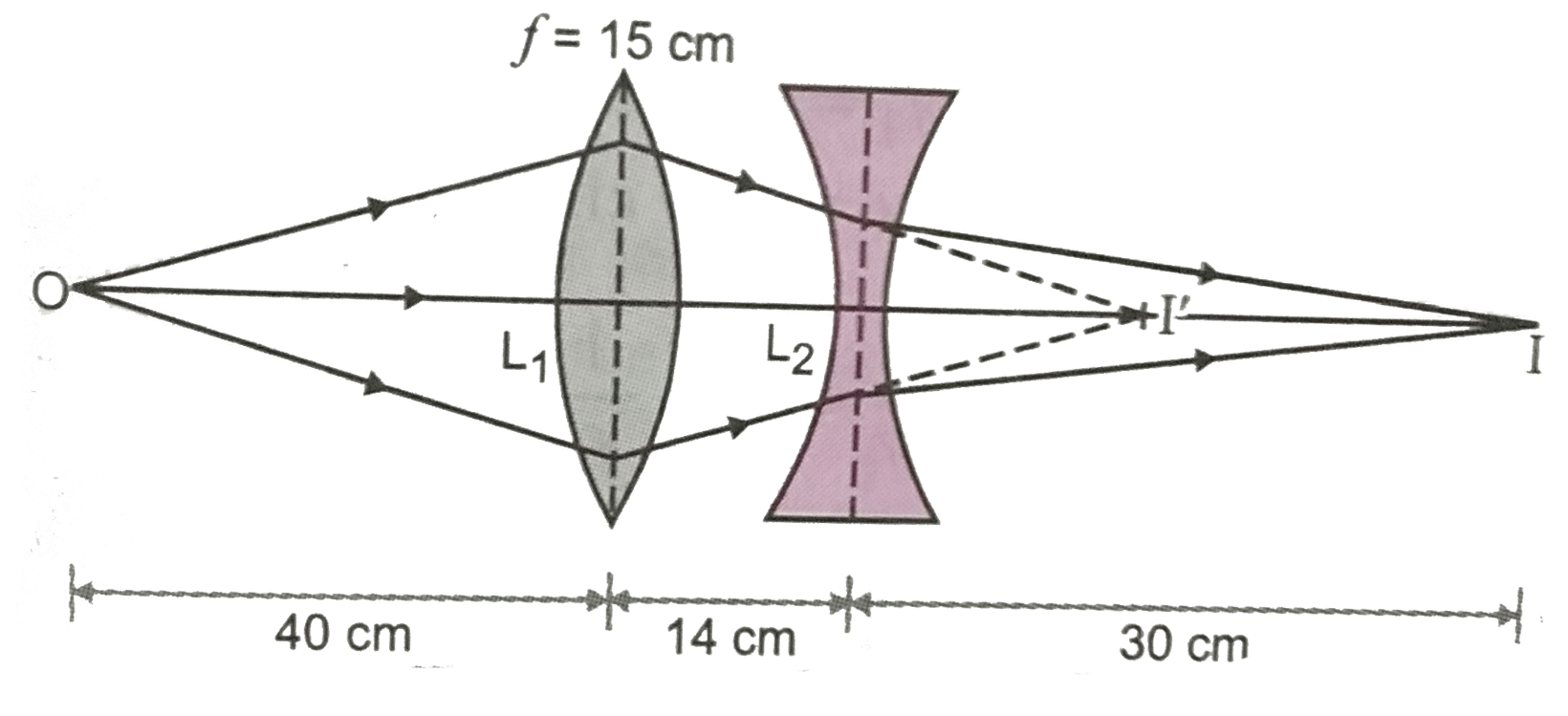
Use the following ray diagram, Fig. 6(b).56 to calculate focal length of lens L2.
View SolutionA source an an observer are at rest w.r.t ground. Which of the following quantities will remain same, if wind blows from source to observer ?
View SolutionConsider the rays shown in figure, as paraxial. The image of the virtual point object O formed by the lens LL is

View SolutionThe speed of sound in air is Both the source and observer are moving towards each other with equal speed u. The speed of wind is w from source to observer. Then, the ratio (ff0)of the apparent frequency to the actual frequency is given by
View SolutionTwo sources give interference pattern which is observed on a screen, D distance apart from the sources. The fringe width is 2 w . If the distance D is now doubled, the fringe width will
View Solution
