There is a thin conducting wire carrying current. What is the value of magnetic field induction at any point on the conductor itself?
To determine the value of the magnetic field induction at any point on a thin conducting wire carrying current, we can follow these steps:
Step 1: Understand the Concept of Magnetic Field Due to a Current-Carrying Wire
The magnetic field (B) generated by a current-carrying conductor can be calculated using the Biot-Savart Law, which states that the magnetic field due to a small segment of current-carrying wire (dl) at a point in space is proportional to the current (I) and inversely proportional to the square of the distance from the segment to the point.
Step 2: Apply the Biot-Savart Law
The Biot-Savart Law is given by:
B=μ0I4π∫dl×^rr2
where:
- μ0 is the permeability of free space,
- I is the current,
- dl is the differential length element of the wire,
- ^r is the unit vector from the wire element to the point where the magnetic field is being calculated,
- r is the distance from the wire element to the point.
Step 3: Analyze the Situation at the Wire Itself
When we consider the magnetic field at any point on the wire itself, the position vector ^r from the wire element dl to the point on the wire is either in the same direction or directly opposite to dl. This means that the angle θ between dl and ^r is either 0 degrees or 180 degrees.
Step 4: Evaluate the Cross Product
The magnetic field contribution from the wire element at that point can be expressed as:
B=μ0I4πdl×^rr2
Since the cross product dl×^r will be zero when θ=0∘ or θ=180∘ (because sin(0)=0 and sin(180)=0), we find that:
B=0
Conclusion
Thus, the magnetic field induction at any point on the conductor itself is zero.
---
The magnetic field (B) generated by a current-carrying conductor can be calculated using the Biot-Savart Law, which states that the magnetic field due to a small segment of current-carrying wire (dl) at a point in space is proportional to the current (I) and inversely proportional to the square of the distance from the segment to the point.
The Biot-Savart Law is given by:
B=μ0I4π∫dl×^rr2
where:
- μ0 is the permeability of free space,
- I is the current,
- dl is the differential length element of the wire,
- ^r is the unit vector from the wire element to the point where the magnetic field is being calculated,
- r is the distance from the wire element to the point.
When we consider the magnetic field at any point on the wire itself, the position vector ^r from the wire element dl to the point on the wire is either in the same direction or directly opposite to dl. This means that the angle θ between dl and ^r is either 0 degrees or 180 degrees.
The magnetic field contribution from the wire element at that point can be expressed as:
B=μ0I4πdl×^rr2
Since the cross product dl×^r will be zero when θ=0∘ or θ=180∘ (because sin(0)=0 and sin(180)=0), we find that:
B=0
Thus, the magnetic field induction at any point on the conductor itself is zero.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Conceptual Problems (d)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Very Short Answer Questions (a)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Along the direction of current carrying wire, the value of magnetic field is ?
AzeroBinfinityCdepends on the length the wireDuncertain
What is the form of magnetic field lines due to a straight current-carrying conductor?
View SolutionWhat is the shape of the magnetic field lines due to a straight current carrying conductor ?
View SolutionWhat is the form of magnetic field lines due to a straight current-carrying conductor?
View SolutionTwo semi infinitely long straight current carrying conductors are held in the form as shown in figure. One common end of them is at the origin. If both the conductors carry same current I, find the value of the magnetic field induction at a point (a, b).
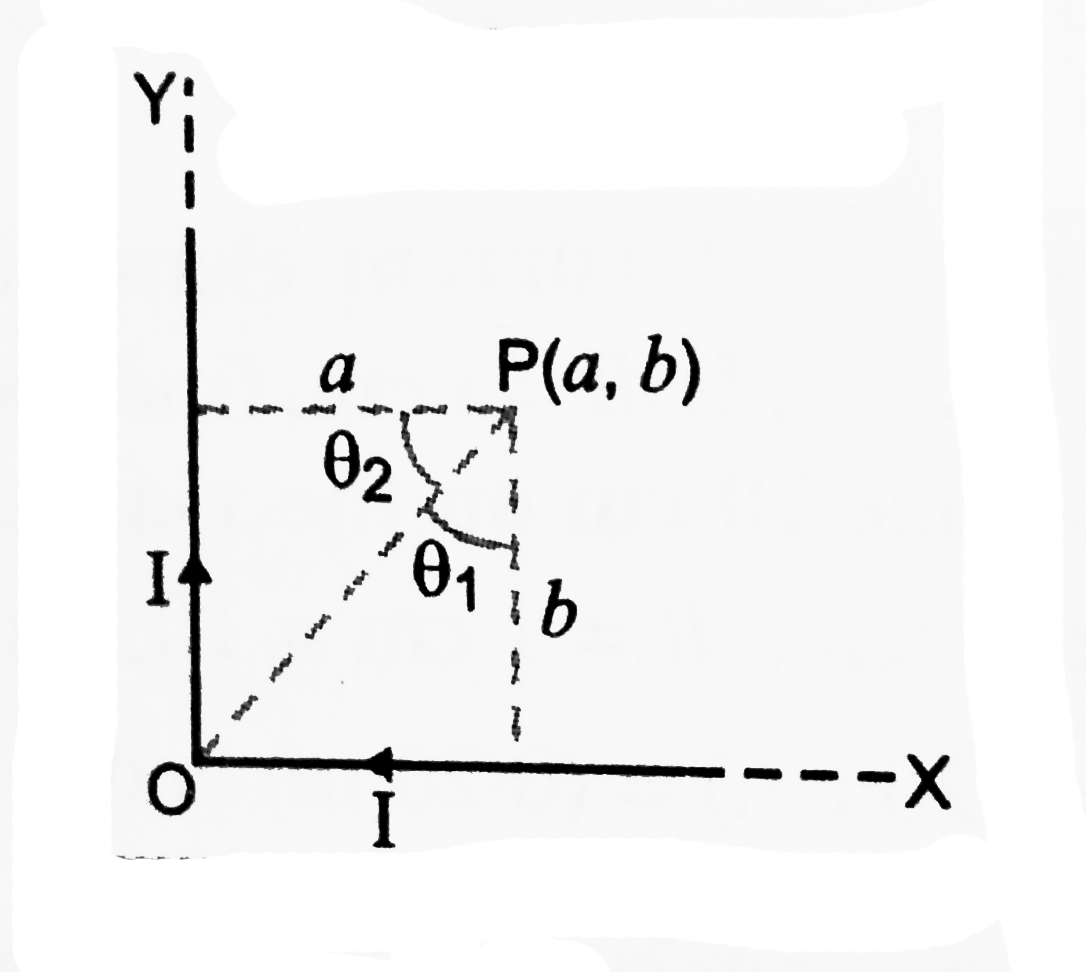 View Solution
View SolutionWrite the relation for the magnetic field induction at a point due to a linear conductor carrying current and hence deduce the relation for the magnetic field induction at a point due to a very long linear conductor carrying current.
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
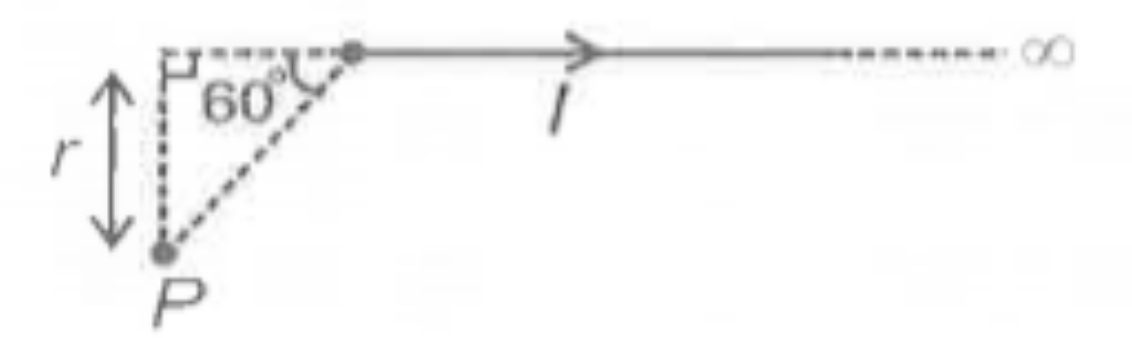 View Solution
View SolutionA long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View Solution

