Two parallel coaxial circular coils of equal radius R and equal number of turns N carry equal currents I in the same direction and are separated by a distance 2R. Find the magnitude and direction of the net magnetic field produced at the mid-point of the line joining their centres.
To solve the problem of finding the net magnetic field produced at the midpoint of the line joining the centers of two parallel coaxial circular coils, we can follow these steps:
1. Identify the Setup:
- We have two parallel circular coils, each with radius R and number of turns N.
- Both coils carry the same current I in the same direction.
- The distance between the centers of the coils is 2R.
2. Determine the Midpoint:
- The midpoint between the two coils is located at a distance R from each coil (since the total distance is 2R).
3. Magnetic Field Due to One Coil:
- The formula for the magnetic field B at a distance x along the axis of a circular coil is given by:
B=μ0NIR22(R2+x2)3/2
- Here, μ0 is the permeability of free space.
4. Calculate the Magnetic Field from Each Coil at the Midpoint:
- For Coil 1 (located at −R):
- The distance x from Coil 1 to the midpoint is R.
- Thus, the magnetic field B1 at the midpoint due to Coil 1 is:
B1=μ0NIR22(R2+R2)3/2=μ0NIR22(2R2)3/2=μ0NIR22(2√2R3)=μ0NI4√2R
- For Coil 2 (located at +R):
- The distance x from Coil 2 to the midpoint is also R.
- Thus, the magnetic field B2 at the midpoint due to Coil 2 is:
B2=μ0NIR22(R2+R2)3/2=μ0NI4√2R
5. Direction of the Magnetic Fields:
- Since both coils carry current in the same direction, the magnetic fields B1 and B2 at the midpoint will be in the same direction (using the right-hand rule).
6. Calculate the Net Magnetic Field:
- The net magnetic field Bnet at the midpoint is the sum of the two magnetic fields:
Bnet=B1+B2=μ0NI4√2R+μ0NI4√2R=2μ0NI4√2R=μ0NI2√2R
Final Answer:
The magnitude of the net magnetic field at the midpoint is:
Bnet=μ0NI2√2R
Direction:
The direction of the net magnetic field is along the axis of the coils, in the direction determined by the right-hand rule based on the current flow.
- We have two parallel circular coils, each with radius R and number of turns N.
- Both coils carry the same current I in the same direction.
- The distance between the centers of the coils is 2R.
- The midpoint between the two coils is located at a distance R from each coil (since the total distance is 2R).
- The formula for the magnetic field B at a distance x along the axis of a circular coil is given by:
B=μ0NIR22(R2+x2)3/2
- Here, μ0 is the permeability of free space.
- For Coil 1 (located at −R):
- The distance x from Coil 1 to the midpoint is R.
- Thus, the magnetic field B1 at the midpoint due to Coil 1 is:
B1=μ0NIR22(R2+R2)3/2=μ0NIR22(2R2)3/2=μ0NIR22(2√2R3)=μ0NI4√2R
- The distance x from Coil 2 to the midpoint is also R.
- Thus, the magnetic field B2 at the midpoint due to Coil 2 is:
B2=μ0NIR22(R2+R2)3/2=μ0NI4√2R
- Since both coils carry current in the same direction, the magnetic fields B1 and B2 at the midpoint will be in the same direction (using the right-hand rule).
- The net magnetic field Bnet at the midpoint is the sum of the two magnetic fields:
Bnet=B1+B2=μ0NI4√2R+μ0NI4√2R=2μ0NI4√2R=μ0NI2√2R
The magnitude of the net magnetic field at the midpoint is:
Bnet=μ0NI2√2R
The direction of the net magnetic field is along the axis of the coils, in the direction determined by the right-hand rule based on the current flow.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Conceptual Problems (d)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Very Short Answer Questions (a)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by B=μ0IR2N2(x2+R2)3/2
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel coaxial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R and is given by B=0⋅72μ0NIR approximately.
[Such as arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]View SolutionFor a circular coil of radius R and N carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by
B=μ0IR2N2(x2+R2)3/2
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coil of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by ,
B=0.72μ0NIR , approximately.
[Such an arrangment to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]View Solution
Knowledge Check
- Question 1 - Select One
Two identical coils each of radius R and each carrying a current I in the same direction are placed along a common axis and separated by distance R. At the midpoint between the two coils the
Amagnetic field is zeroBmagnetic field is 0.8 sqrt(0.8)mu""_0I/RCsecond derivative of magnetic fieldDfirst derivative of magnetic field dB/dx=0 - Question 2 - Select One
Two identical coils each of radius R and each carrying a current I in the same direction are placed along a common axis and separated by distance R. At the midpoint between the two coils the
Amagnetic field is zeroBmagnetic field is 0.8 sqrt(0.8)mu""_0I/RCsecond derivative of magnetic fieldDfirst derivative of magnetic field dB/dx=0
Consider two parallel co-axial circular coils of equal radius R, and number of turn N, carrying equal currents in the same direction and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B=0.72μ0NIR, approximately. [Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
View SolutionTwo small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
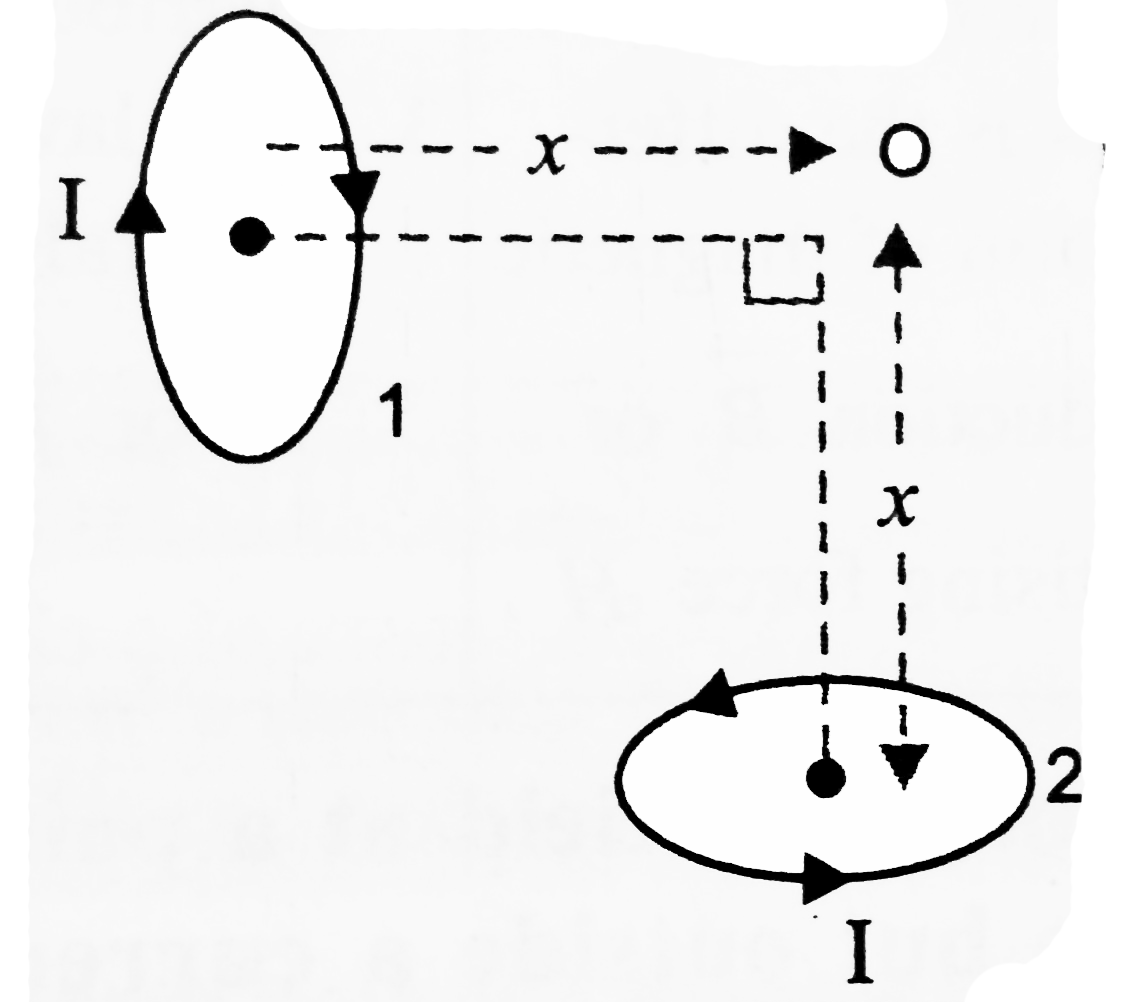 View Solution
View SolutionTwo parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionFig shows two current-carrying wires 1 and 2. Find the magnitudes and directions of the magnetic field at points P,Q and R.
 View Solution
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in fig. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
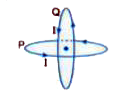 View Solution
View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.
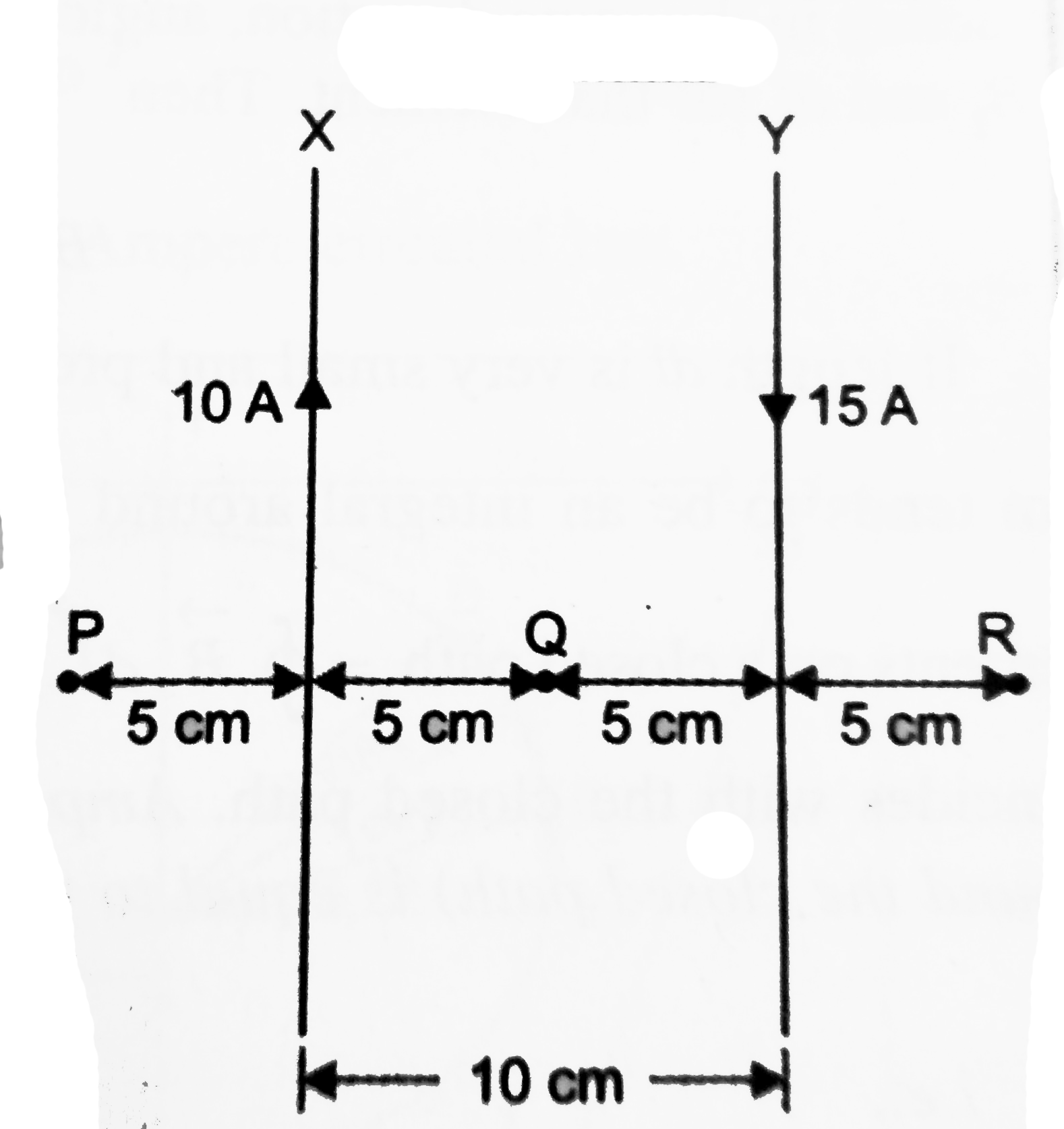 View Solution
View Solution

