A non-conducting thin disc of radius R charged uniformly over one side with surface density $σ$ , rotates about its axis with an angular velocity $ω$ . Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.

Video Solution

Text Solution

Verified by Experts

(a) Consider an elementary ring of the disc of radius x and thickness $d x$ shown by shaded portion in figure. Charge on the elementary ring, $d q = σ 2 π x d x$ . Current due to this element is

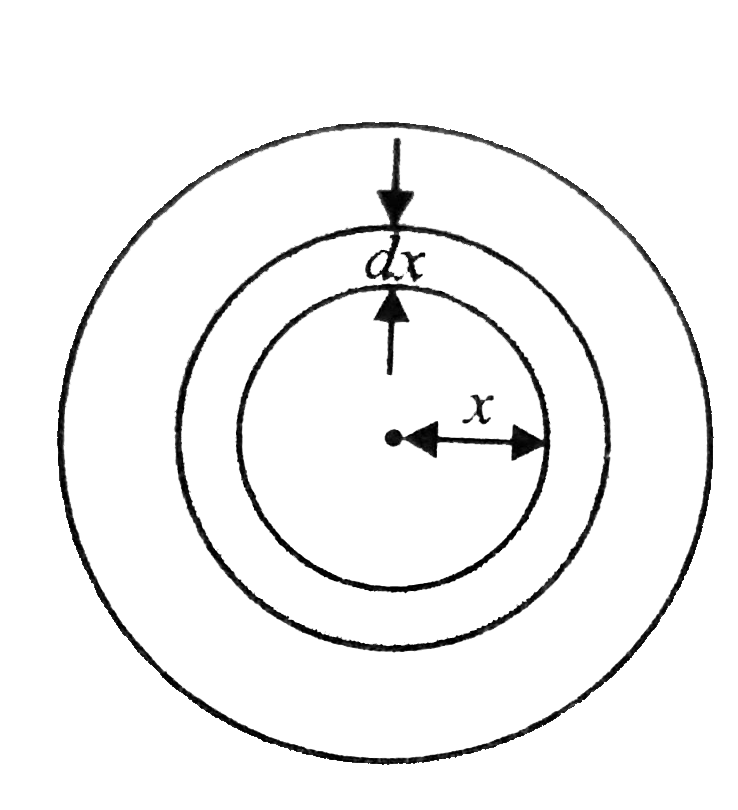
$d I = \frac{σ 2 π x d x}{T} = (σ 2 π x d x) \frac{ω}{2 π} = σ ω x d x$
Magnetic field induction at the centre, due to this element is
$d B = \frac{μ_{0}}{4 π} \frac{2 π d I}{x} = \frac{μ_{0}}{2} \frac{d I}{x} = \frac{μ_{0}}{2} \frac{σ ω x d x}{x} = \frac{μ_{0}}{2} σ ω d x$
Magnetic field induction at the centre of the disc will be, $B = \int_{0}^{R} \frac{μ_{0}}{2} σ ω d x = \frac{μ_{0}}{2} σ ω R$
(b) Magnetic dipole moment of teh elementary ring, $d M = d I \times π x^{2} = (σ ω x d x) \times π x^{2}$
$= σ π ω x^{3} d x$
Magnetic dipole moment of the whole disc will be
$M = σ π ω \int_{0}^{R} x^{3} d x = \frac{1}{4} σ π ω R^{4}$

Updated on:21/07/2023