Two long and parallel straight wires A and B carrying currents of 8⋅0A and 5⋅0A in the same direction are separated by a distance of 4⋅0cm. Estimate the force on a 10cm section of wire A.
To solve the problem, we will follow these steps:
Step 1: Understand the Given Data
We have two long parallel wires A and B carrying currents I1=8A and I2=5A respectively. The distance between the wires is R=4cm=0.04m. We need to find the force on a 10cm section of wire A.
Step 2: Formula for Force Between Parallel Wires
The force per unit length F/L between two parallel wires carrying currents can be calculated using the formula:
F/L=μ0I1I22πR
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Step 3: Substitute the Values into the Formula
Substituting the values into the formula:
F/L=(4π×10−7)×(8)×(5)2π×(0.04)
Step 4: Simplify the Expression
We can simplify the expression:
F/L=(4×8×5)×10−72×0.04
Calculating the numerator:
4×8×5=160
Thus:
F/L=160×10−70.08
Now, calculating 0.08:
0.08=8×10−2
So:
F/L=160×10−78×10−2=20×10−5N/m=2×10−4N/m
Step 5: Calculate the Force on a 10 cm Section
Now, we need to find the force on a 10cm section (which is 0.1m):
F=(FL)×L=(2×10−4N/m)×(0.1m)=2×10−5N
Step 6: Determine the Nature of the Force
Since both currents are in the same direction, the force will be attractive.
Final Answer
The force on a 10cm section of wire A is 2×10−5N and the force is attractive.
---
We have two long parallel wires A and B carrying currents I1=8A and I2=5A respectively. The distance between the wires is R=4cm=0.04m. We need to find the force on a 10cm section of wire A.
The force per unit length F/L between two parallel wires carrying currents can be calculated using the formula:
F/L=μ0I1I22πR
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Substituting the values into the formula:
F/L=(4π×10−7)×(8)×(5)2π×(0.04)
We can simplify the expression:
F/L=(4×8×5)×10−72×0.04
Calculating the numerator:
4×8×5=160
Thus:
F/L=160×10−70.08
Now, calculating 0.08:
0.08=8×10−2
So:
F/L=160×10−78×10−2=20×10−5N/m=2×10−4N/m
Now, we need to find the force on a 10cm section (which is 0.1m):
F=(FL)×L=(2×10−4N/m)×(0.1m)=2×10−5N
Since both currents are in the same direction, the force will be attractive.
The force on a 10cm section of wire A is 2×10−5N and the force is attractive.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Conceptual Problems (d)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Very Short Answer Questions (a)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
Two long and parallel straight wire A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
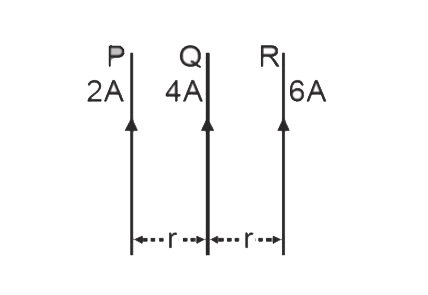
View SolutionP, Q and R long parallel straight wires in air, carrying currents as shown. The direction of resultant force on R is :-
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two long and parallel straight wires A and B carrying currents of 0.8 A and 5.0 A in the same direction are separated by distance of 0.4 cm. What is the force on a 10 cm section of wire A ?
A10−5NB2×10−5NC3×10−5ND4×10−5N - Question 2 - Select One
Two long and parallel straight wires A and B are carrying currents of 4A and 7A in the same directions are separated by a distance of 5cm. The force acting on a 8cm section of wire A is
A3×10−6NB6×10−6NC9×10−6ND12×10−6N - Question 3 - Select One
Two long parallel copper wires carry currents of 5A each in opposite directions. If the wires are separated by a distance of 0.5m , then the force between the two wires is
A10−5N, attractiveB10−5N repulsiveC2×10−5N, attractiveD2×10−5N,repulsive
Two parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionTwo straight wires A and B of lengths 10m and 16m and carrying currents 4⋅0A and 5⋅0A respectively in opposite directiions, lie parallel to each other 4⋅0cm apart, Comute the force on a 10cm long section of the wire B near its centre.
View SolutionTwo straight wires A and B of lengths 10 m and 12 m carrying currents of 4.0 A and 6.0 A respectively in opposite direction, lie parallel to each other at a distance of 3.0 cm. The force on a 15 cm section of the wire B near its centre is
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View Solution

