An electron and a position are released from (0, 0, 0) and $(0, 0, 1 \cdot 5 R)$ respectively, in a uniform magnetic field $\to B = B_{0} ˆ i$ , each with an equal momentum of magnitude $p = e B R$ . Under what conditions on the direction of momentum will the orbits be non-intersecting circles?

Video Solution

Text Solution

Verified by Experts

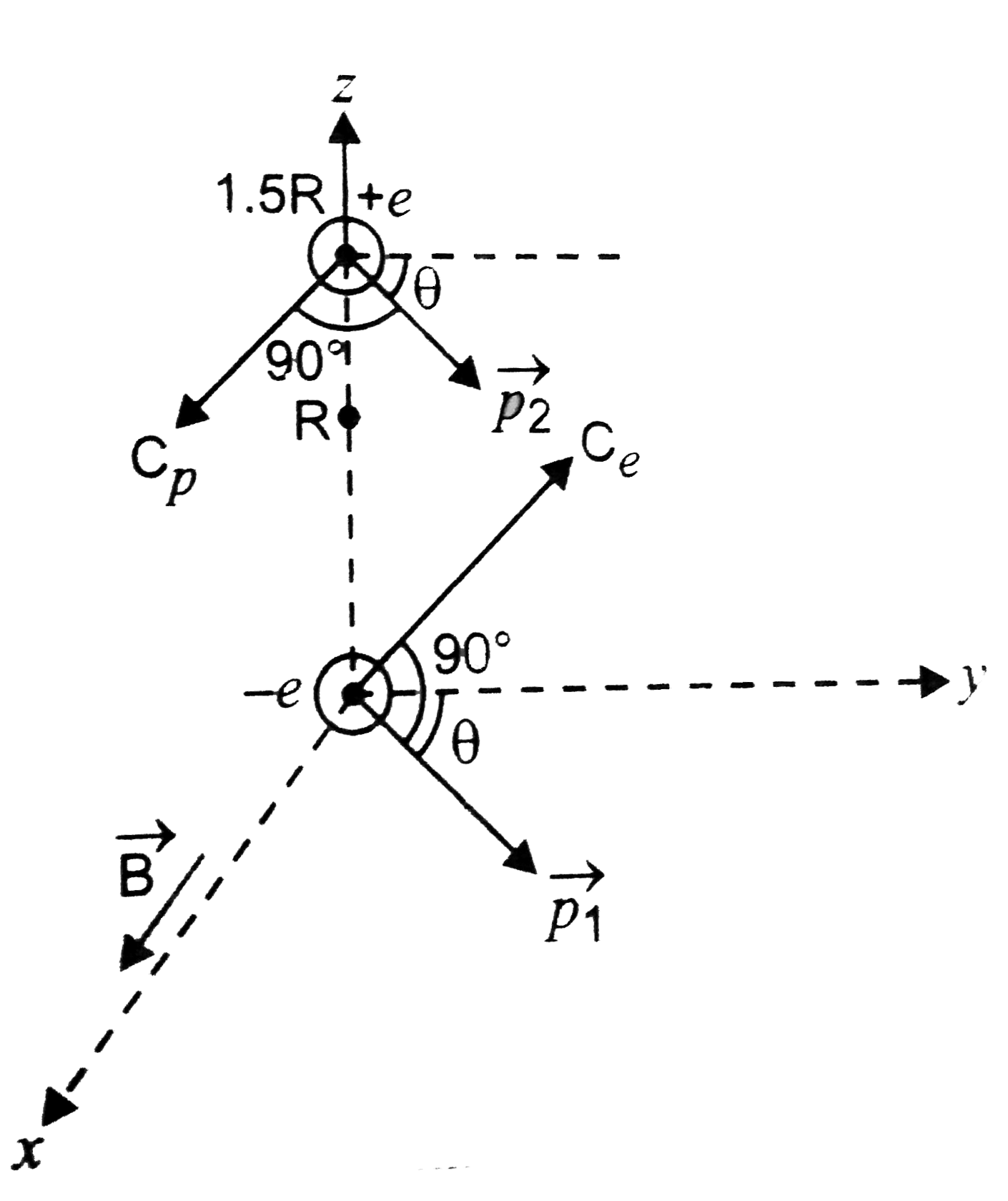
Here, $\to B (= B_{0} ˆ i)$ is acting along the x-axis. For a circular orbit, the momentum of the electron and position are in y-z plane. Let ${\to p}_{1}$ and ${\to p}_{2}$ be the momentum of the electron and position respectively. Both of them due to same momentum $(= e B R)$ move on circular orbits, each of radius R, but in opposite sense.
Let ${\to p}_{1}$ make an angle $θ$ with the y-axis and ${\to p}_{2}$ must make the same angle $θ$ with y-axis. The centres of the respective circular orbits must be perpendicular to the momenta at a distance R. Let the centre of the circular orbit of the electron be at $C_{e}$ and of the position be at $C_{p}$ .
The coordinates of $C_{e}$ is $(0, R sin θ, R cos θ)$
The coordinates of $C_{p}$ is $[0, - R sin θ, (\frac{3}{2} R - R cos θ)]$
The two circular orbits will not intersect if the distance between their two centre is greater than 2R.
Let d be the distance between $C_{p}$ and $C_{e}$ . Then
$d^{2} = {[- R sin θ - (R sin θ)]}^{2} + {[(\frac{3}{2} R - R cos θ)} {- (R cos θ)]}^{2}$
$= 4 R^{2} {sin}^{2} θ + \frac{9}{4} R^{2} - 6 R^{2} cos θ + 4 R^{2} {cos}^{2} θ = 4 R^{2} ({sin}^{2} θ + {cos}^{2} θ) + \frac{9}{4} R^{2} - 6 R^{2} cos θ$
$= \frac{25}{4} R^{2} - 6 R^{2} cos θ$
The two circular orbits will not intersect each other if $d > 2 R$ or $d^{2} > 4 R^{2}$
$∴ \frac{25}{4} R^{2} - 6 R^{2} cos θ > 4 R^{2}$ or $\frac{25}{4} - 6 cos θ > 4$ or $\frac{9}{4} > 6 cos θ$ or $cos θ < 3 / 8$

Updated on:21/07/2023

A proton is fired from origin with velocity $\to v = v_{0} ˆ j + v_{0} ˆ k$ in a uniform magnetic field $\to B = B_{0} ˆ j$ .
Aits z-coordinate can never be negative
Bits x-coordinate can never be negative
Cits x-and z-coordinates cannot be zero at the same time
Dits y-coordinate will be proportional to its time of flight
Two point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
A $\frac{2 q d}{4 π ε_{0} {(d^{2} + a^{2})}^{3 / 2}} ˆ k$
B $\frac{q d}{4 π ε_{0} {(d^{2} + a^{2})}^{3 / 2}} ˆ k$
C $\frac{- 2 q d}{4 π ε_{0} {(d^{2} + a^{2})}^{3 / 2}} ˆ k$
D $\frac{- q d}{4 π ε_{0} {(d^{2} + a^{2})}^{3 / 2}} ˆ k$
A charged particle of mass m and charge q is released from rest the position $(x_{0}, 0)$ in a uniform electric field $E_{0} ˆ j$ . The angular momentum of the particle about origin.
Ais zero
Bis constant
Cincreases with time
Ddecreases with time