If the current density in a linear conductor of radius 'a' varies with r according to relation , where k is a constant and r is the distance of a point from the axis of conductor. Find the magnetic field induction at a point distance r from the axis, when (i) and (ii) .
The correct Answer is:(i) (ii)
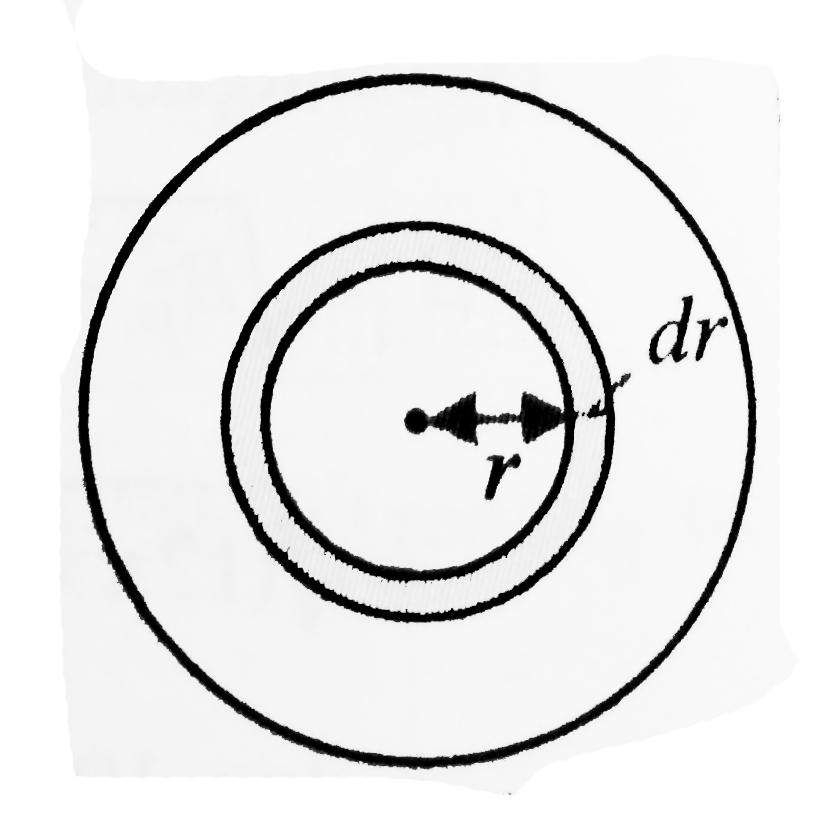
(i) Consider an elementary ring of radius r thickness dr whose centre lies on the axis of the conductor. Area of the elementary ring, . Current passing through the elementary ring is
Total current passing through the closed path of radius r is,
Using Ampere circuital law, we have
or
(ii) If , then net current through the closed path of radius r is,
Using Ampere circuital law, we have
or
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
Suppose that the current density in a wife of radius a varies with r according to J=Kr2, where K is a constant and r is the distance from the axis of the wire. Find the megnetic field at a point distance r from the axis when (a) r < a and (b) r > a
 View Solution
View SolutionSuppose that the current density in a wire of radius a varius with r according to Kr2 where K is a constant and r is the distance from the axis of the wire. Find the magnetic field at a point at distance r form the axis when (a) rlta and (b) rgta.
View Solution
Knowledge Check
- Question 1 - Select One
Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
If the current density in a linear conductor of radius a varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor, find the magnetic field induction at a point distance r from the axis when rlta. Assume relative permeability of the conductor to be unity.Aμ0ka44rBμ0kr32Cμ0kπa42rDμ0ka34 - Question 2 - Select One
The current density in a wire of radius a varies with radial distance r as J=J0r2a, where J0 is a constant. Choose the incorrect statement.
ATotal current passing through the cross-section of the wire isI=πJ0a32BTotal current passing through the cross-section of the wire isI=3πJ0a32CThe field at a distance r gt a is B=μ0J0a34rDThe field at a distance r gt a is B=μ0J0a34a - Question 3 - Select One
Let r be the distance of a point on the axis of a bar magnet from its centre. The magnetic field at such a point is proportional to
A1rB1/r^2C1/r^3Dnone of these
An infinitely long cylindrical shell ofinner radius r1 and outer radius r2 is charged in its volume with a volume charge density which varies with distance from axis of cylinder as p=blrC/m3 which C is a positive constant and r is the distance from axis of cylinder. Find the electric field intensity at a point P at a distance x from axis of cylinder
View SolutionA cylindrical conductor of radius 'R' carries a current 'i'. The value of magnetic field at a point which is R/4 distance inside from the surface is 10T. Find the value of magnetic field at point which is 4R distance outside from the surface
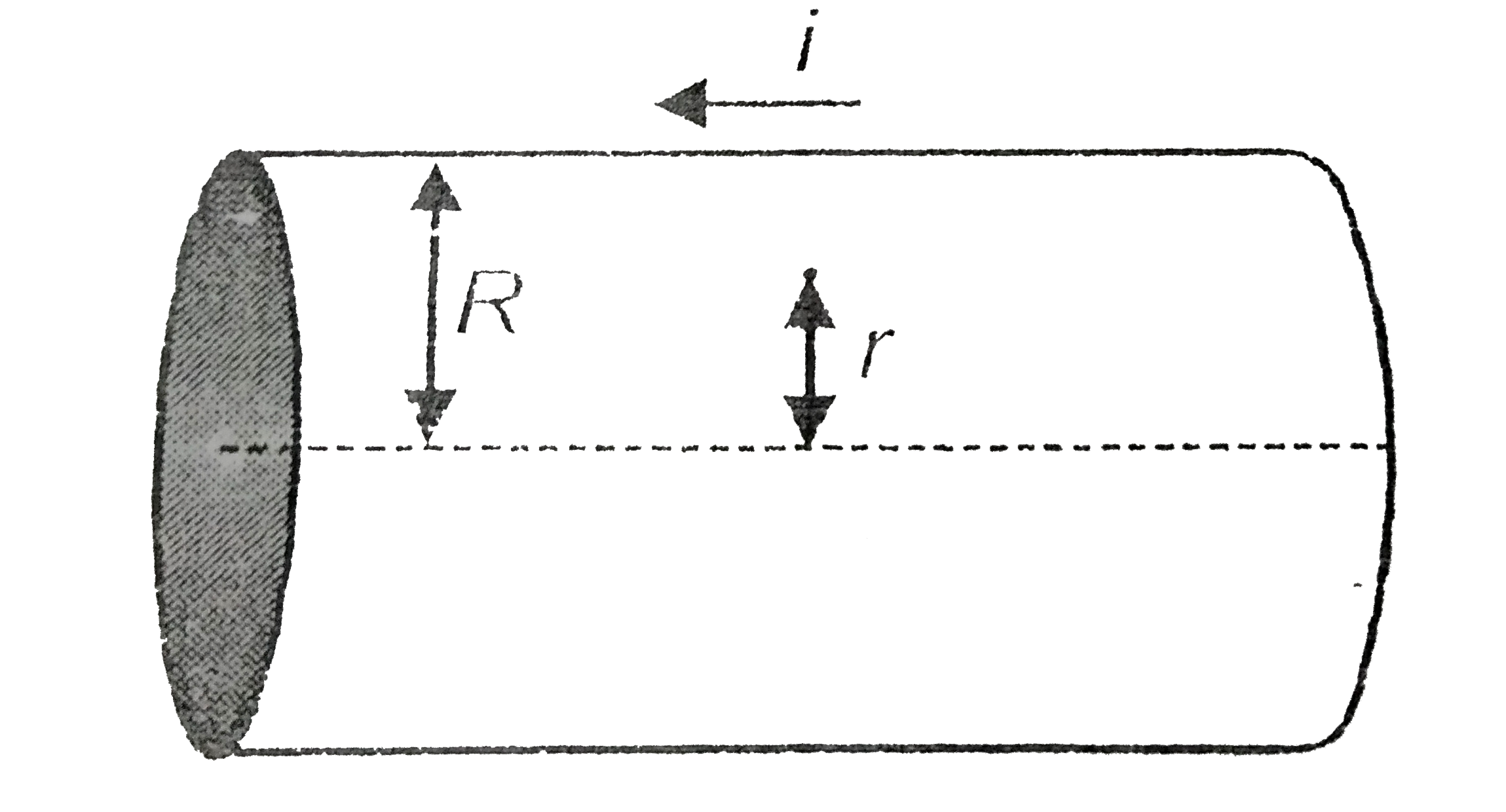
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
 View Solution
View SolutionA current 'I' flows along an infinitely long straight conductor. If 'r' is the perpendicular distance of a point from the lower end of the conductor, then the magnetic induction B is given by
View Solutionlet B be the magnetic field at a point between the two conductors, at a distance x from the axis. Let B2 be the magnetic field at a point outside conductor, at a distance 2x from the axis
View Solution

