(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
(a) The magnetic energy is
UB=12LI2
As, B=μ0NIl, therefore,
I=Blμ0N∴UB=12L(Blμ0N)2
Using L=μ0N2Al , we get,
UB=12(μ0N2Al)(Blμ0N)2
UB=B22μ0Al
(b) The volume that contains flux, V=A×l
∴ Magnetic energy per unit volume,
uB=UBV=B22μ0
It is known that electrostatic energy stored per unit volume in a parallel plate capacitor is
uE=12∈0E2
In both the cases. energy is directly proportional to the square of the field strenth.
Note that Eqna. (ii) and (iii) have been derived for special cases -- a solenoid and a parallel plate capacitor respectively. But they are valid for any region of space in which a magnetic field or/and an electric field exists.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions
2 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Advance Problems For Competitions
1 Video
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions
1 Video
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question
5 Videos
Similar Questions
(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
View Solution(a) Obtain the expression for the magnetic energy stored in a solenoid, due to the current I flowing in it, in terms of magnetic field B, area of cross-section A and length l of the solenoid.
(b) How is this magnetic energy per unit volume compared with the electrostatic energy per unit volume stored in a parallel plate capacitor ?
View Solution
Knowledge Check
In the figure magnetic energy stored in the coil is
 AzeroBinfiniteC25 joulesDnone of the above
AzeroBinfiniteC25 joulesDnone of the aboveMagnetic field energy stored in a coil is
ALi2B12LiCLiD12Li2
The total electrostatic energy stored in both the capacitor is
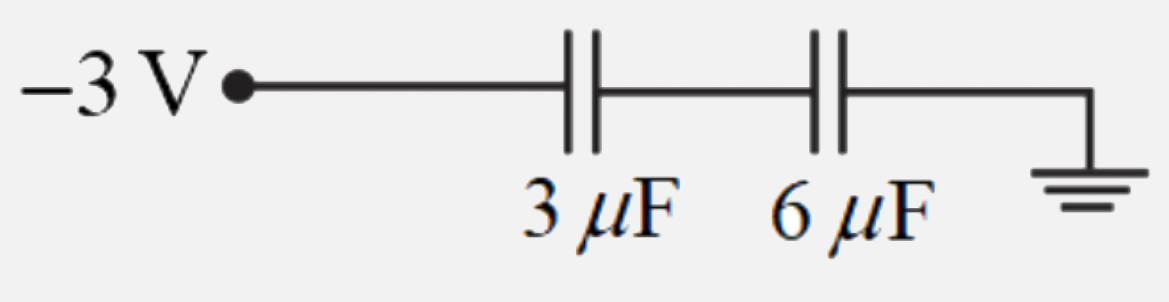
View SolutionMagnetic energy stored per unit volume in a magnetic field is _____.
View SolutionWhat is expression for magnetic energy stored in an inductor. Compare it with the electrostatic energy stored in a capacitor.
View SolutionStarting from the expression for the energy W=1/2LI2, stored in a solenoid of self-inductance L to build up the current I, obtain the expression for the magnetic energy in terms of the magnetic field B, area A and length l of the solenoid having n number of turns per unit length. Hence, show that the energy density is given by B2/2μ0.
View SolutionHow does the magnetic length of a magnet compare to the geometric length of a magnet?
View SolutionThe total electrostatic energy stored in both the capacitors (in μJ) is
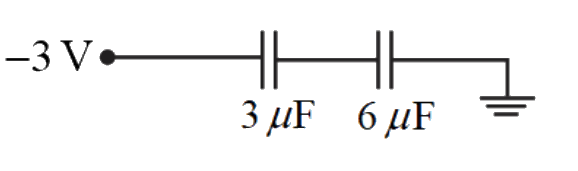
View Solution
