In a closed loop, which has some inductance but negligible resistance, uniform but time varying magentic field is applied directed into the plane of the loop. Variation of field with time is shown in Fig. Initially current in loop was zero. Then .
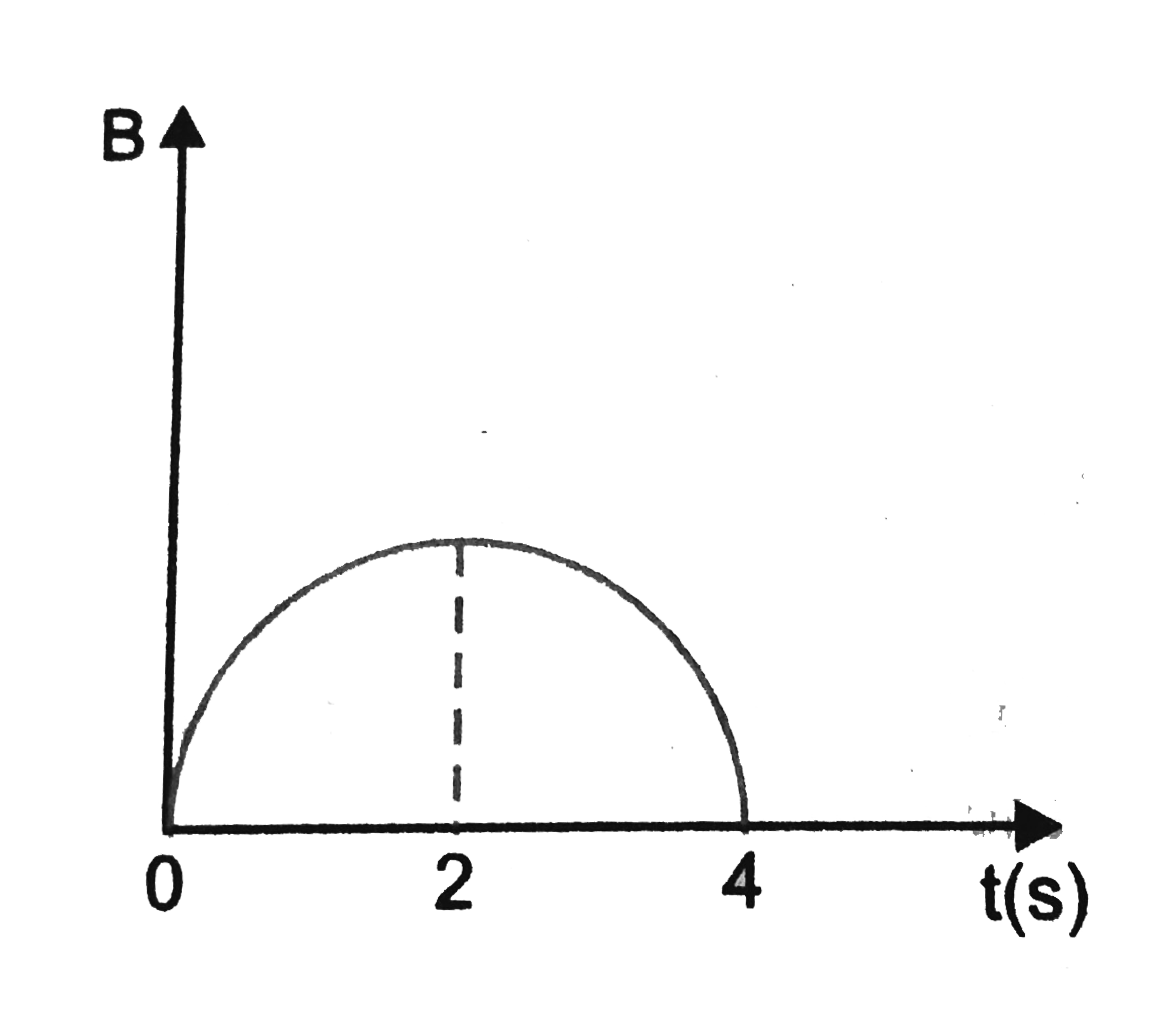
emf induced in the loop is zero at
current in the loop will be maximum at
direciton of emf in the loop will not change at
none of above
The correct Answer is:A
As and ,
therefore, from Fig. we find that at
.
The flux increases from 0 to 2 sec and it decreases from to .
Therefore, the direction of e.m.f. in the loop is reversed at .
Choice (a) is correct.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - JEE Mains Ad..(Multiple Choice Question)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Value Based Questions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
A closed loop with the geometry shown in Fig. 3.9 is placed in a uniform magnetic field direction into the plane of the paper. If the magnetic field decreases with time, determine the direction of the induced emf in this loop.
 View Solution
View SolutionA superconducting loop of radius R has self inductance L.A uniform & constant magnetic field B is applied perpendicular to the plane of the loop.Initially current in this loop is zer.The loop is rotated about its diameter by 180∘.Find the current in the loop after rotation.
View Solution
Knowledge Check
- Question 1 - Select One
In non-uniform magnetic field in certain direction, current loop is placed
Anet force and net torque on loop is zero.Bnet force may be zero but net torque non zeroCnet torque may be zero but net force is non zero.Dneither net force nor net torque is zero. - Question 2 - Select One
A wire is bent to form the double loop shown in figure. There is a uniform magnetic field directed into the plane of the loop. If the magnitude of this field is decreasing, current will flow from:
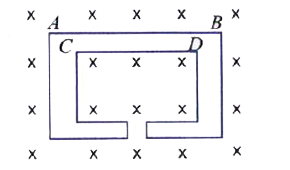 AA to B and C to DBB to A and D to CCA to B and D to CDB to A and C to D
AA to B and C to DBB to A and D to CCA to B and D to CDB to A and C to D - Question 3 - Select One
A wire is bent to form the double loop shown in figure. There is a uniform magnetic field directed into the plane of the loop. If the magnitude of this field is decreasing current will flow from:
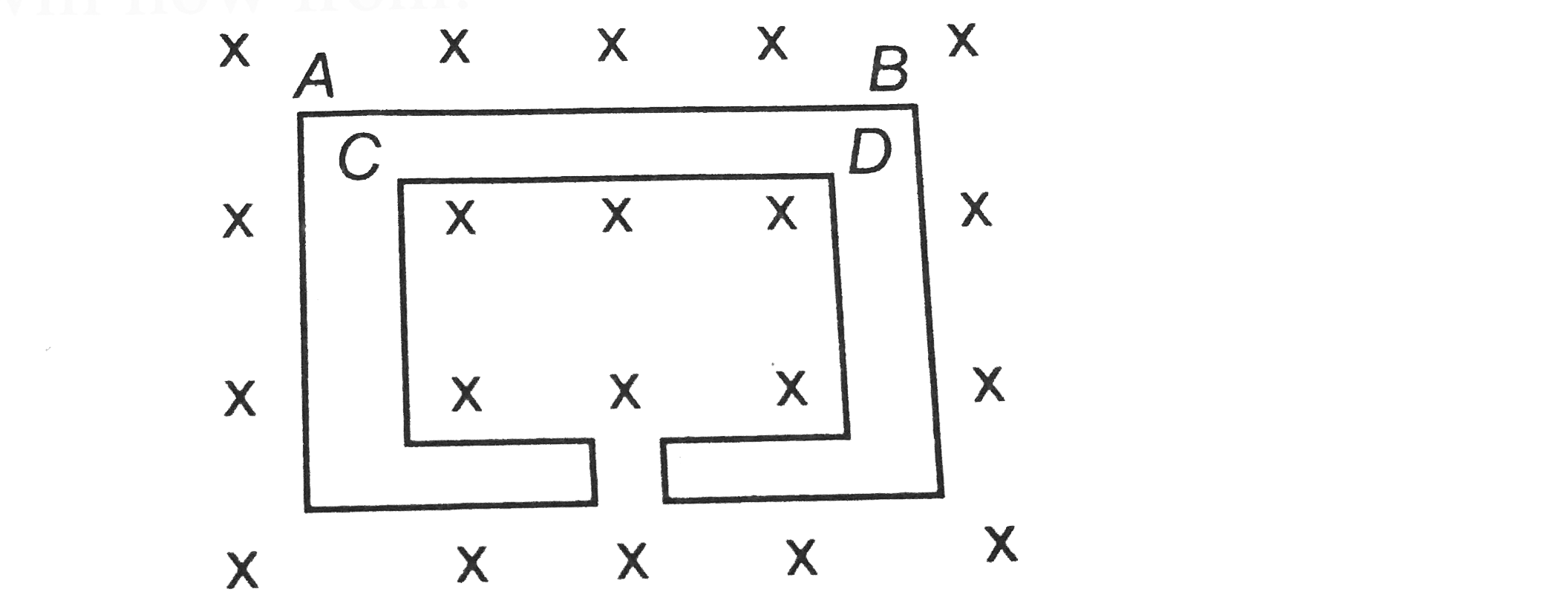 AA to B and C to DBB to A and D to CCA to B and D to CDB to A and C to D
AA to B and C to DBB to A and D to CCA to B and D to CDB to A and C to D
The magnetic field through a circular loop of wire 12 cm in radius and 8.5 ohm resistance, changes with time as shown in Fig. The magnetic field is perpendicular to the plane of the loop. Calculate the induced current in the loop and plot is as a function of time.
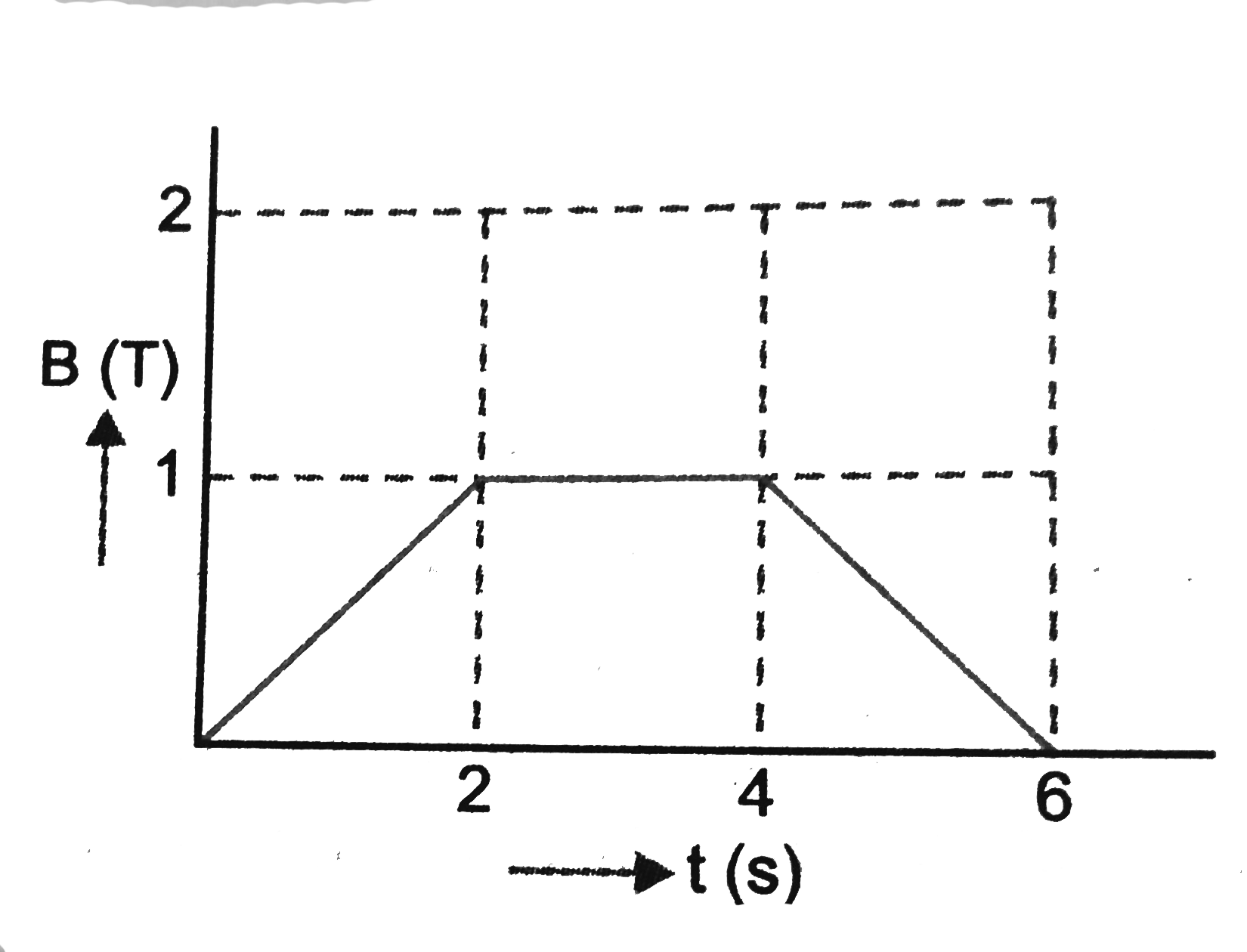 View Solution
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is constant and t is time. The induced current flowing through loop is
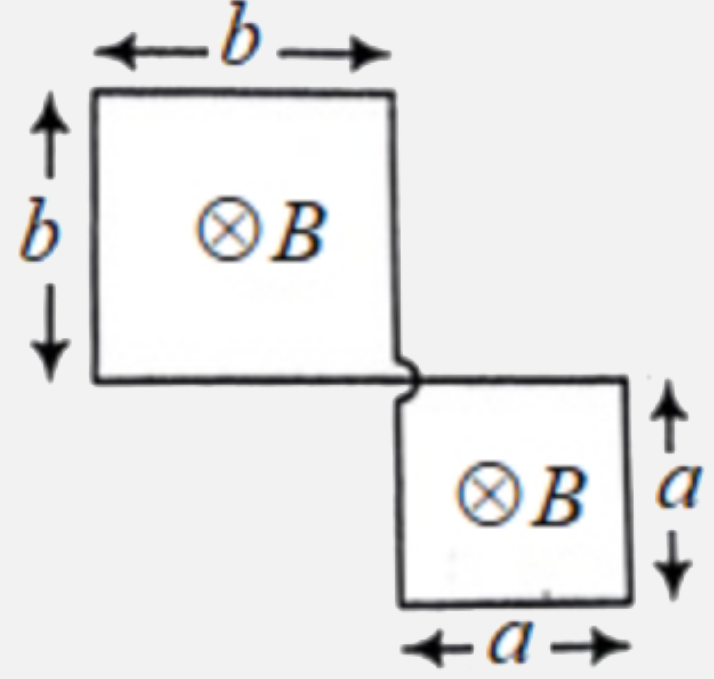 View Solution
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is a constant and t is time. The induced current flowing through loop is
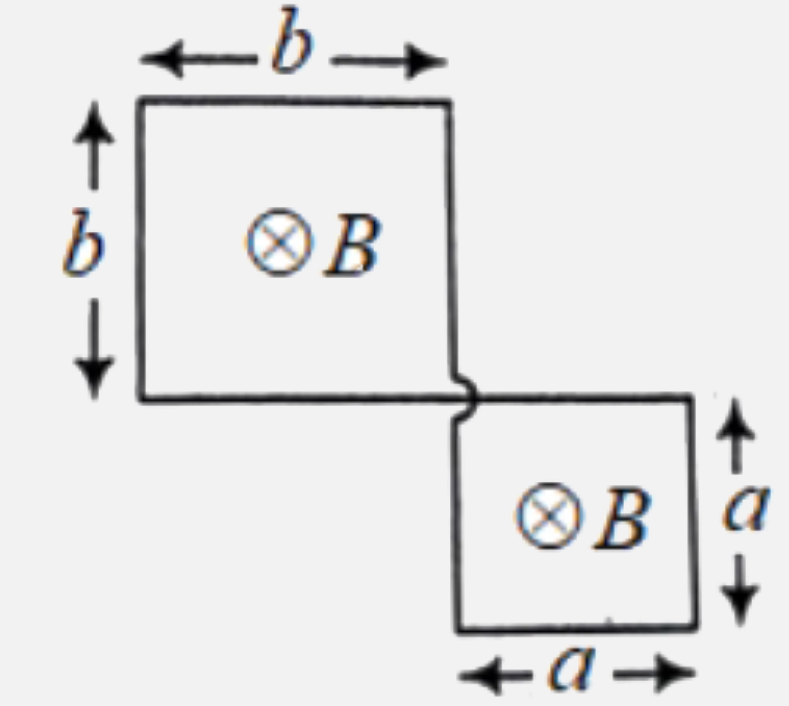 View Solution
View SolutionA closed loop of cross-sectional area 10−2m2 which has inductance L=10mH and negligible resistance is placed ti time- varying magnetic field. Figure shows the variation of B with time for the intervel 4s. The field is perpendicular to the plane of the loop (given at t=0, B=0, I=0). The value of the maximum current induced in the loop is
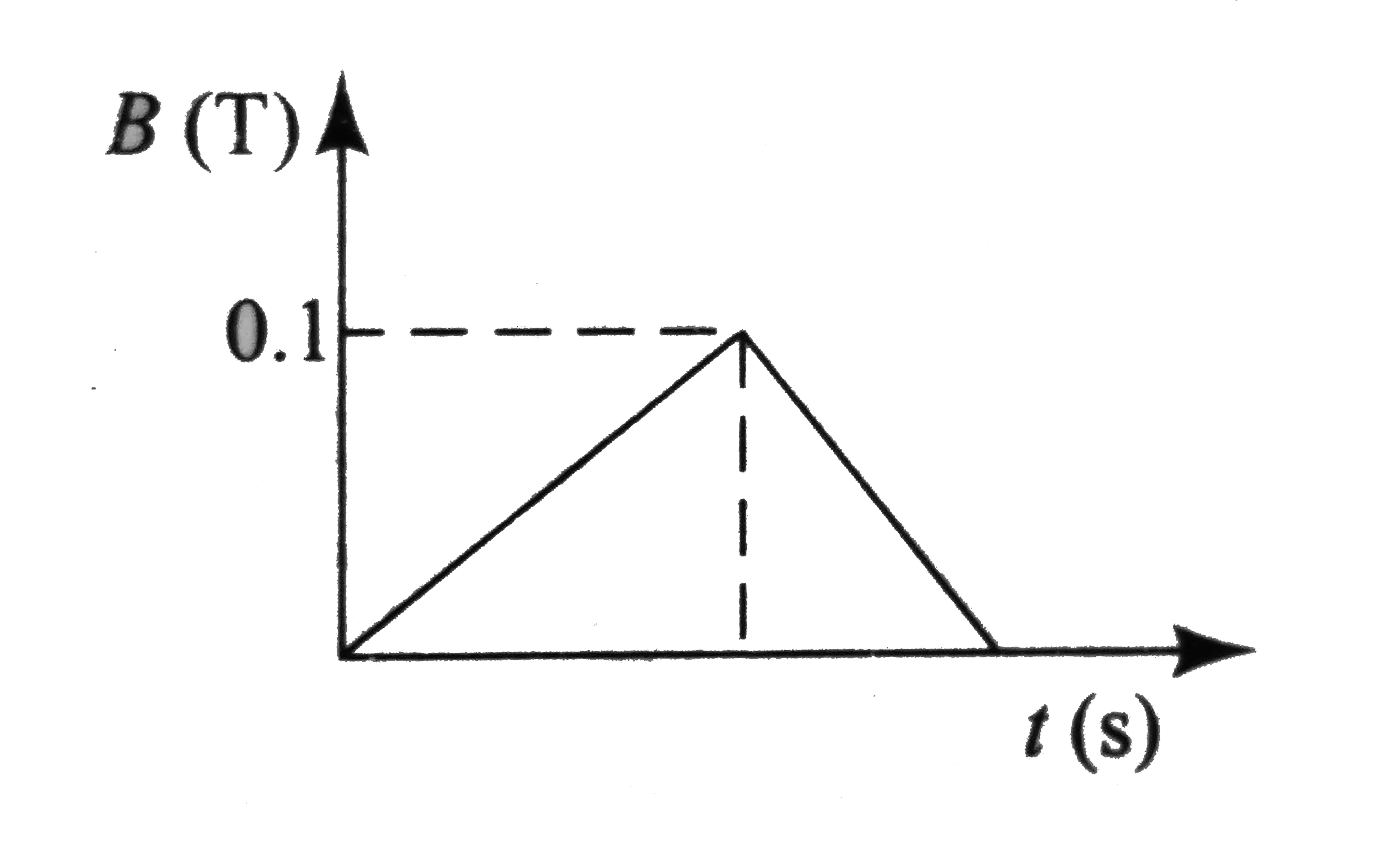 View Solution
View SolutionA loop shown in the figure is immersed in the varying magnetic field B=B0t, directed into the page. If the total resistance of the loop is R, then the direction and magnitude of induced current in the inner circle is
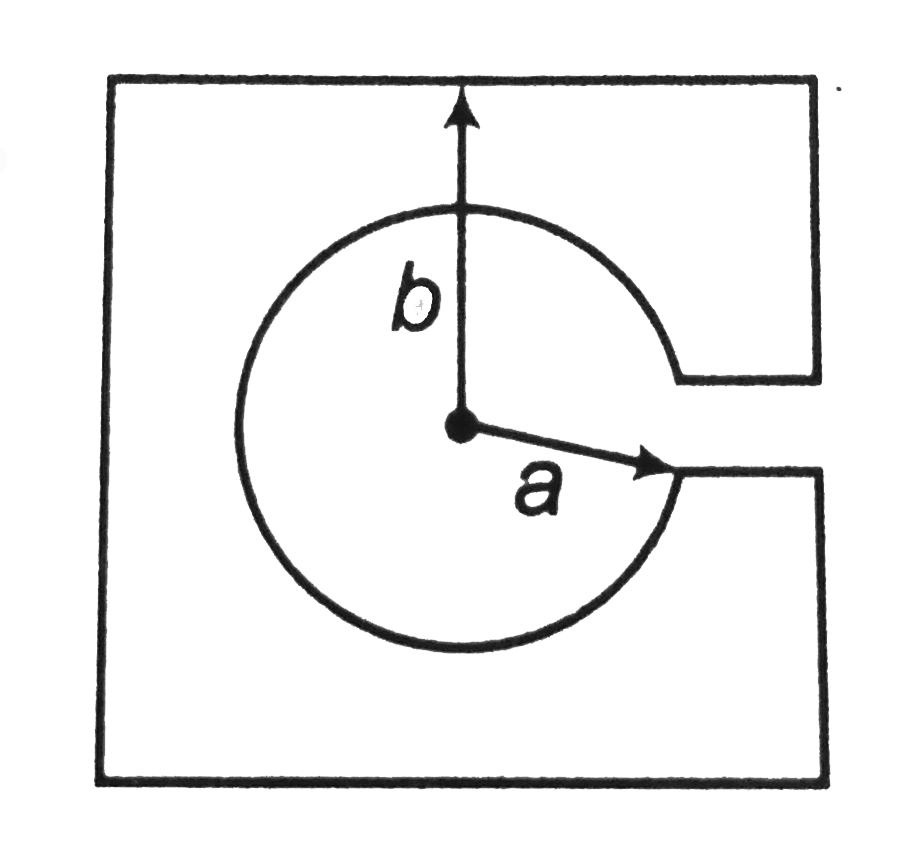 View Solution
View Solution

