Assertion : The magnetic flux through a closed surface containing a bar magnet is zero.
Reason : Gauss's law applies in the case of electric flux only.
A
B
C
D
The correct Answer is:C
To solve the given question, we will analyze both the assertion and the reason provided.
Step 1: Analyze the Assertion
The assertion states that "The magnetic flux through a closed surface containing a bar magnet is zero."
- When a bar magnet is placed inside a closed surface, the magnetic field lines emerge from the north pole and enter the south pole.
- For every magnetic field line that exits the closed surface from the north pole, there is a corresponding line that enters the surface at the south pole.
- Therefore, the total magnetic flux through the closed surface is indeed zero because the number of lines entering equals the number of lines exiting.
Conclusion for Step 1: The assertion is true.
Step 2: Analyze the Reason
The reason states that "Gauss's law applies in the case of electric flux only."
- Gauss's law is a fundamental principle in electromagnetism that applies to both electric and magnetic fields.
- For electric fields, Gauss's law states that the electric flux through a closed surface is proportional to the charge enclosed within that surface.
- Similarly, Gauss's law for magnetism states that the magnetic flux through a closed surface is zero, which aligns with our assertion regarding the bar magnet.
Conclusion for Step 2: The reason is false.
Final Conclusion
- The assertion is true, while the reason is false. Therefore, the correct answer to the question is that the assertion is correct, but the reason is incorrect.
The assertion states that "The magnetic flux through a closed surface containing a bar magnet is zero."
- For every magnetic field line that exits the closed surface from the north pole, there is a corresponding line that enters the surface at the south pole.
- Therefore, the total magnetic flux through the closed surface is indeed zero because the number of lines entering equals the number of lines exiting.
The reason states that "Gauss's law applies in the case of electric flux only."
- For electric fields, Gauss's law states that the electric flux through a closed surface is proportional to the charge enclosed within that surface.
- Similarly, Gauss's law for magnetism states that the magnetic flux through a closed surface is zero, which aligns with our assertion regarding the bar magnet.
- The assertion is true, while the reason is false. Therefore, the correct answer to the question is that the assertion is correct, but the reason is incorrect.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - JEE Mains Ad..(Multiple Choice Question)
1 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions
1 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Value Based Questions
2 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question
5 Videos
Similar Questions
Knowledge Check
The net magnetic flux through any closed surface, kept in a magnetic field is
AzeroBμ04πC4πμ0D4μ0πThe net magnetic flux through any closed surface, kept in a magnetic field is
AzeroBμ04πC4πμ0D4μ0πThe electric flux through the surface
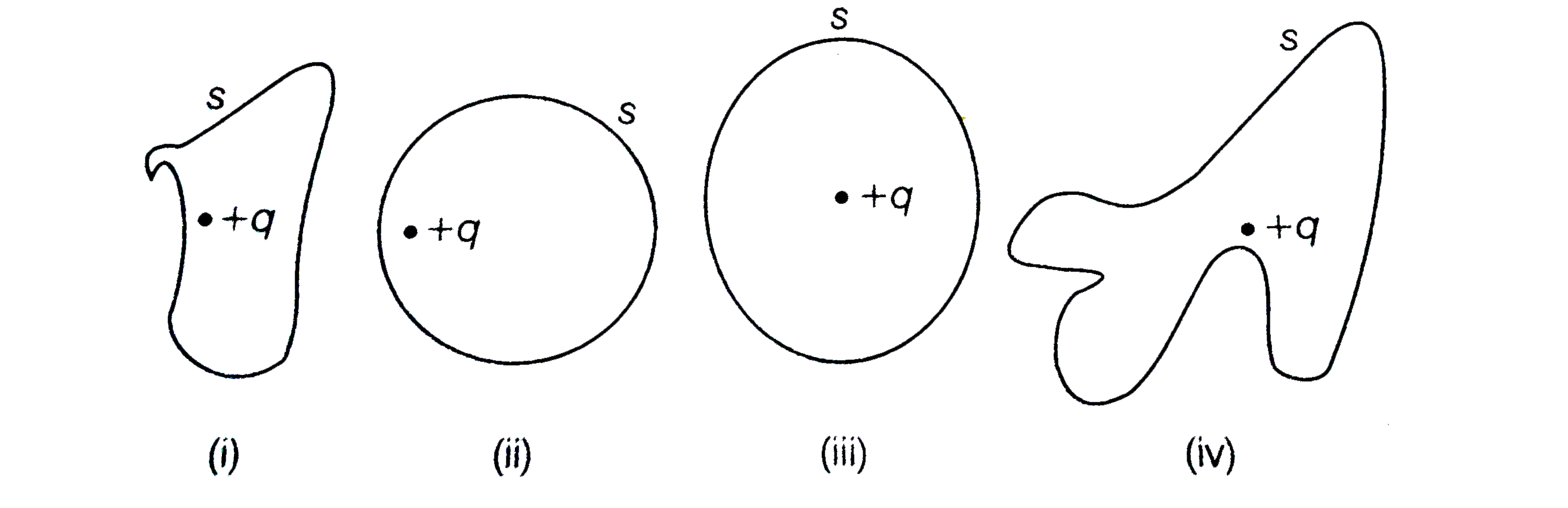 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
What do you mean by magnetic flux through a surface?
View SolutionThe electric flux through the surface

View SolutionThe electric flux through a closed Gaussian surface depends upon
View SolutionIf the net electric flux through a closed surface is zero, then we can infer
View SolutionGauss' law states that net flux through a closed surface is proportional to
View Solution