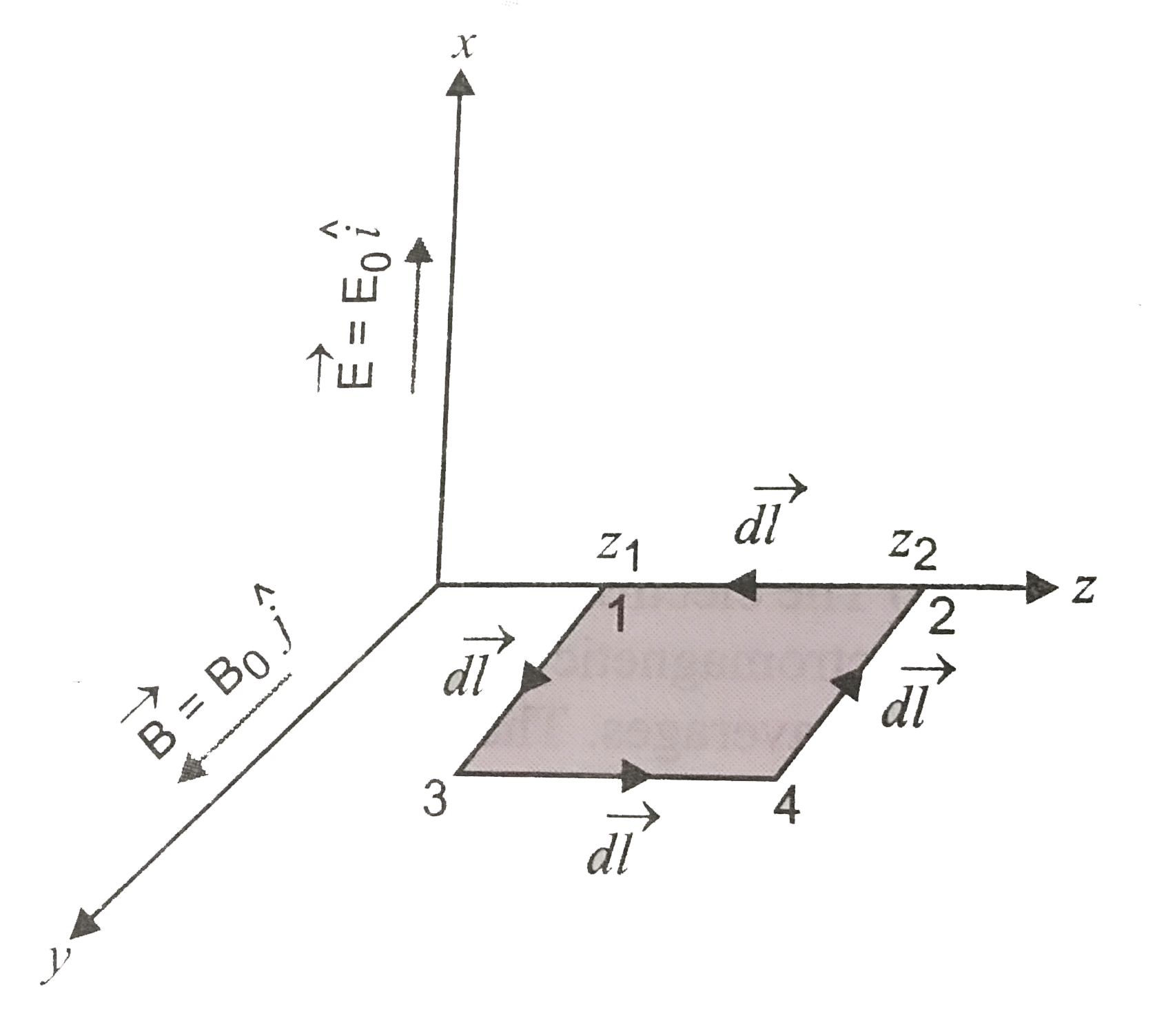
A plane EM wave travelling in vacuum along z-direction is given by $E = E_{0} sin (k z - ω t) ˆ i and B = B_{0} sin (k z - ω t) ˆ j$
(i) Evaluate $\int E . d l$ over the rectangular loop 1234 shown in figure.
(ii) Evaluate $\int B . d s$ over the surface bounded by loop 1234.
(iii) Use equation $\int E . d l = \frac{- d ϕ_{B}}{d t}$ to prove $\frac{E_{0}}{B_{0}} = c .$
(iv) By using similar proces and the equation
$\int B . d l = μ_{0} I + ε_{0} \frac{d ϕ_{E}}{d t},$ prove that $c \frac{1}{\sqrt{μ_{0} ε_{0}}}$

Video Solution

Text Solution

Verified by Experts

(i) During the propagation of e.m. wave along z-axis, let electric field vector $\to E$ be along x-
axis and magnetic field vector $\to B$ be along y-axis i.e., $\to E = E_{0} ˆ i and \to B = B_{0} ˆ j$ . Line
integral of $\to E$ over the closed rectangular, path 1234 in x-z plane is
$\oint \to E . \to d l = \int_{1}^{2} \to E . \to d l + \int_{2}^{3} \to E . \to d l + \int_{3}^{4} \to E . \to d l + \int_{4}^{1} \to E . \to d l$
$= \int_{1}^{2} E d l {cos 90}^{\circ} + \int_{2}^{3} E d l {cos 0}^{\circ} + \int_{3}^{4} E d l {cos 90}^{\circ} + \int_{4}^{1} E d l {cos 180}^{\circ}$
$= 0 + E_{z_{2}} h + 0 - E_{z_{1}} h = E_{z_{2}} - E_{z_{1}} = E_{0} h [sin (k z_{2} - ω t) - sin (k z_{1} - ω t)] ... ... (i)$
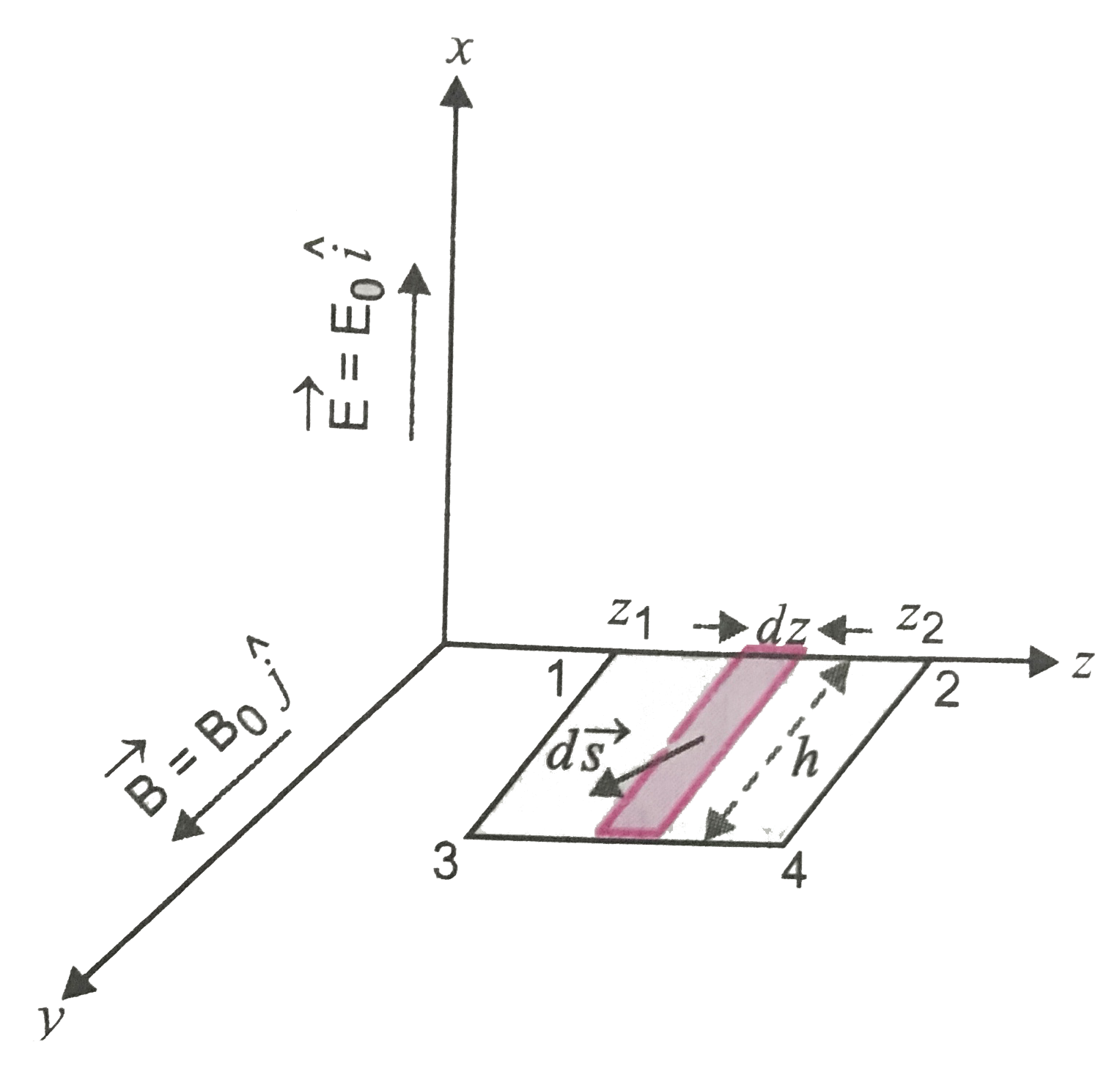
(ii) For evaluting $\oint \to B . \to d l$ over the surface bounded by
loop1234, let us consider a rectangle 1234 be made of small
strips. One small strip of area ds=h dz is shown in fig.
$\oint_{Surface bounded by strips 1234} \to B . \to d s = \oint B d s {cos 0}^{\circ} = \oint B d s$
$= \int_{z_{1}}^{z_{2}} B_{0} sin (k z_{2} - ω t) h d z$
$= - \frac{B_{0} h}{k} [cos (k z_{2} - ω t) - cos (k z_{1} - ω t) ... . . (i i)$
(iii) Given, $\oint \to E . \to d l = - \frac{d ϕ_{B}}{d t} = - \frac{d}{d t} \oint \to B . \to d s$
Puting the values from (i) and (ii), we get,
$E_{0} h [sin (k z_{2} - ω t) - sin (k z_{1} - ω t)]$
$= - \frac{d}{d t} [- \frac{B_{0} h}{k} {cos (k z_{2} - ω t) - cos (k z_{1} - ω t)}]$
$= \frac{B_{0} h}{k} ω [sin (k z_{2} - ω t) - sin (k z_{1} - ω t)}]$
or $E_{0} = \frac{B_{0} ω}{k} = B_{0} c (∵ \frac{ω}{k} = c) or E_{0} / B_{0} = c$
(iv) For evaluting $\oint \to B . \to d l$ , let us consider a loop 1342
in y-z plane as shown in fig.
$\oint \to B . \to d l = \oint_{1}^{3} \to B . \to d l + \oint_{3}^{4} \to B . \to d l + \oint_{4}^{2} \to B . \to d l + \oint_{2}^{1} \to B . \to d l$
$\int_{1}^{3} B d l {cos 0}^{\circ} + \int_{3}^{4} B d l {cos 90}^{\circ} + \int_{4}^{2} B d l {cos 180}^{\circ} + \int_{2}^{1} B d l {cos 90}^{\circ} = \int_{1}^{3} B d l + 0 - \int_{4}^{2} B d l + 0$
$= B_{z_{1}} h - B_{z_{2}} h = h (B_{z_{1}} - B_{z_{2}}) = B_{0} h [sin (k z_{1} - ω t) - sin (k z_{2} - ω t)] ... . (i i i)$
To evalute $ϕ_{E} = \oint \to E . \to d s$ , let us consider the rectangle
1342 to be made up of strips, each of area ds=hdz. fig.
$ϕ_{E} = \oint \to E . \to d s = \oint E d s {cos 0}^{\circ} = \oint E d s$
$\int_{z_{1}}^{z_{2}} E_{0} sin (k z_{1} - ω t) h d z$
$= - \frac{E_{0} h}{k} [cos (k z_{2} - ω t) - cos (k z_{1} - ω t)]$
$∴ \frac{d ϕ_{E}}{d t} = \frac{E_{0} h ω}{k} [sin (k z_{1} - ω t) - sin (k z_{2} - ω t) ... . (i v)$
In the relation, $\oint \to B . \to d l = μ_{0} [1 + ε_{0} \frac{d ϕ_{E}}{d t}]$
I is the conduction current. The value of I=0 (in vacuum) $∴ \oint \to B . \to d l = μ_{0} ε_{0} \frac{d ϕ_{E}}{d t}$
Putting values form (iii) and (iv), we get
$B_{0} h [sin (k z_{1} - ω t) - sin (k z_{2} - ω t)] = μ_{\in}_0 \frac{E_{0} h ω}{k} [sin (k z_{1} - ω t) - sin (k z_{2} - ω t)]$
or $B_{0} h = μ_{0} \in_{0} E_{0} h \frac{ω}{k} or \frac{E_{0}}{B_{0}} \frac{ω}{k} = \frac{1}{μ_{0} \in_{0}} [a s \frac{E_{0}}{B_{0}} = c and ω = c k]$
$∴ c \frac{c k}{k} = \frac{1}{μ_{0} \in_{0}} or c^{2} = \frac{1}{μ_{0} \in_{0}} or c = \frac{1}{\sqrt{μ_{0} \in_{0}}}$

Updated on:21/07/2023