Light from a point source in air falls on a spherical glass surface. If μ=1.5, and radius of curvature =20cm, the distance of light source from the glass surface is 100cm , at what position will the image be formed ? (NCERT Solved Example)
To solve the problem of finding the position of the image formed by a spherical glass surface when light from a point source in air falls on it, we will use the lens maker's formula and the sign conventions for spherical surfaces.
Step 1: Identify the given values
- Refractive index of glass, μ=1.5
- Radius of curvature, R=20cm
- Distance of the light source from the glass surface, u=−100cm (the negative sign indicates that the object is on the same side as the incoming light)
Step 2: Calculate the focal length of the spherical surface
The formula for the focal length f of a spherical surface is given by:
f=R2(μ−1)
Substituting the values:
f=20cm2(1.5−1)=20cm2×0.5=20cm1=20cm
Step 3: Use the lens formula to find the image distance
The lens formula is given by:
1f=1v−1u
Where:
- v is the image distance (to be determined)
- u=−100cm
- f=20cm
Rearranging the lens formula gives:
1v=1f+1u
Substituting the known values:
1v=120+1−100
Calculating the right-hand side:
1v=120−1100=5100−1100=4100=125
Thus,
v=25cm
Step 4: Conclusion
The image is formed at a distance of 25cm on the opposite side of the spherical surface from the light source.
Summary of the Solution:
- The focal length of the spherical surface was calculated using the formula f=R2(μ−1).
- The lens formula was then applied to find the image distance v.
- Refractive index of glass, μ=1.5
- Radius of curvature, R=20cm
- Distance of the light source from the glass surface, u=−100cm (the negative sign indicates that the object is on the same side as the incoming light)
The formula for the focal length f of a spherical surface is given by:
f=R2(μ−1)
Substituting the values:
f=20cm2(1.5−1)=20cm2×0.5=20cm1=20cm
The lens formula is given by:
1f=1v−1u
Where:
- v is the image distance (to be determined)
- u=−100cm
- f=20cm
1v=1f+1u
Substituting the known values:
1v=120+1−100
Calculating the right-hand side:
1v=120−1100=5100−1100=4100=125
Thus,
v=25cm
The image is formed at a distance of 25cm on the opposite side of the spherical surface from the light source.
- The focal length of the spherical surface was calculated using the formula f=R2(μ−1).
- The lens formula was then applied to find the image distance v.
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Very short answer question
5 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - very short answer questions
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Light from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
View SolutionDerive the mathematical relation between refractive indices n1 and n2 of two media and radius of curvature R for refraction at a convex spherical surface. Consider the object to be a point one lying on the principal axis in rarer medium of refractive index nt and a real image formed in the denser medium of refractive index n2. Hence, derive lens maker's formula.
(ii) Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20 cm. The distance of light source from the glass surface is 100 cm. At what position is the image formed ?
View Solution
Knowledge Check
From a point source a light falls on a spherical glass surface (μ=1.5 and radius of curvature =10cm). The distance between point source and glass surface is 50cm. The position of image is
A25cmB50cmC100cmD150cmA point object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at
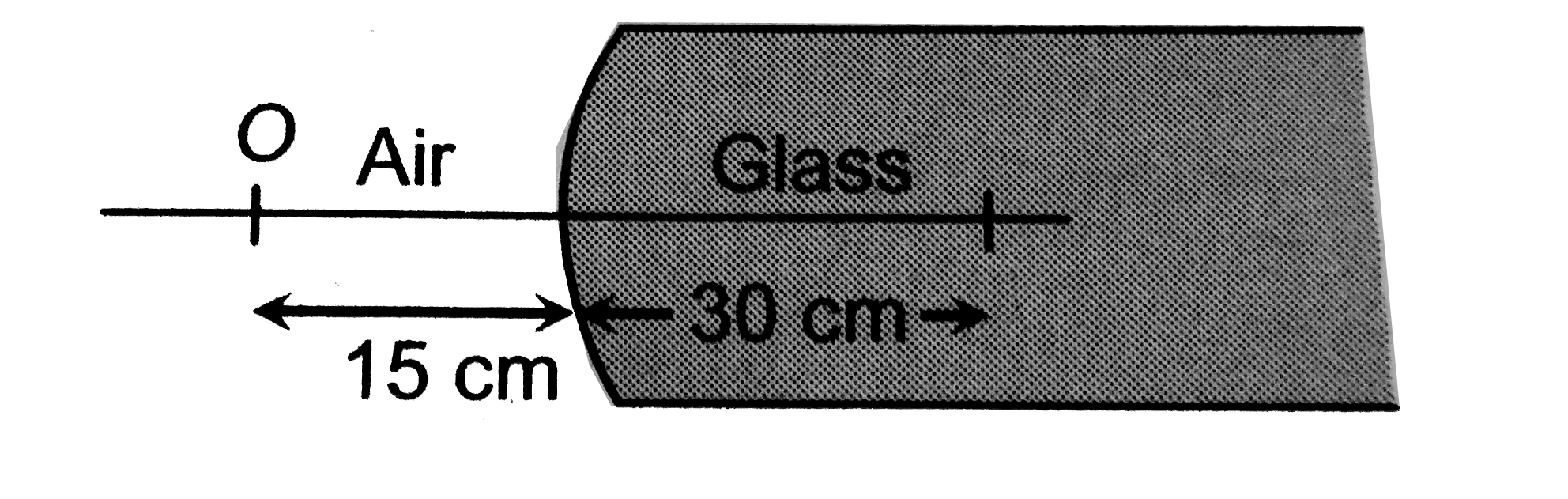 A30 cm lefBinfinityC1 cm to the rightD18 cm to the left
A30 cm lefBinfinityC1 cm to the rightD18 cm to the left
(i) Device the mathematical n between refractive indices n1 and n2 of two radii and radius of curvature R for refraction at a convex shperical surface. Consider the object to be a point since lying on the principal axis in rarer medium of refractive index n1 and a real image formed in the denser medium of refractive index n2. Hence, derive lens marker's formula.
(ii) Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20cm. The distance of light source from the glass surface is 100cm. At what position is the image formed ?
View SolutionLight from a point source in air falls on a convex spherical glass surface (μ=1.5andR=20cm). Calculate position of the image when the light source is at 1m from the glass surface.
View SolutionLight from a point source in air falls on a spherical glass surface μ=1.5andR=20cm. The image is formed at a distance of 100cm from the glass surface in the direction of incident light. Calculate the object distance from the centre of curvature of the spherical surface.
View SolutionA double convex spherical glass has refractive index 1.5 and both radius of curvature 30 cm. A point object is placed at a distance of 120 cm from the spherical glass. What will be the position of the image formed ?
View SolutionA small point objects is placed in air at a distance of 60cm from a convex spherical refractive surface of μ=1.5. If radius of curvature of spherical surface is 25m, calculate the position of the image and the power of the refracting surface.
View SolutionA point source of light is placed in air, 100 cm away from a convex spherical surface, made of material of refractive index 1.5 and having radius of curvature = 20 cm. If the source emits light, at what position from the convex surface image will be formed?
View Solution
