An equiconvex lens of focal length 15cm is cut into two equal halves in thickness. What is the focal length of each half ?
To find the focal length of each half of an equiconvex lens cut into two equal halves, we can follow these steps:
Step 1: Understand the Properties of the Lens
An equiconvex lens has two identical curved surfaces. The focal length (F) of the original lens is given as 15 cm.
Step 2: Use the Lens Maker's Formula
The lens maker's formula for a lens is given by:
1F=(n−1)(1R1−1R2)
Where:
- F is the focal length of the lens,
- n is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
For an equiconvex lens, we have:
- R1=R (positive, since it is convex),
- R2=−R (negative, since it is also convex but considered in the opposite direction).
Step 3: Calculate the Focal Length of the Original Lens
Using the lens maker's formula:
1F=(n−1)(1R−(−1R))=(n−1)(2R)
Given that F=15 cm, we can express this as:
115=(n−1)(2R)
Step 4: Cutting the Lens
When the lens is cut into two equal halves, each half becomes a plano-convex lens. The flat side of the plano-convex lens does not contribute to the curvature.
Step 5: Focal Length of Each Half
For a plano-convex lens, the lens maker's formula simplifies to:
1F′=(n−1)(1R−0)=(n−1)(1R)
Thus, the focal length F′ of each half is:
F′=F2
Since the original focal length F=15 cm, the focal length of each half is:
F′=152=30 cm
Final Answer
The focal length of each half of the lens is 30 cm.
---
An equiconvex lens has two identical curved surfaces. The focal length (F) of the original lens is given as 15 cm.
The lens maker's formula for a lens is given by:
1F=(n−1)(1R1−1R2)
Where:
- F is the focal length of the lens,
- n is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
- R1=R (positive, since it is convex),
- R2=−R (negative, since it is also convex but considered in the opposite direction).
Using the lens maker's formula:
1F=(n−1)(1R−(−1R))=(n−1)(2R)
Given that F=15 cm, we can express this as:
115=(n−1)(2R)
When the lens is cut into two equal halves, each half becomes a plano-convex lens. The flat side of the plano-convex lens does not contribute to the curvature.
For a plano-convex lens, the lens maker's formula simplifies to:
1F′=(n−1)(1R−0)=(n−1)(1R)
Thus, the focal length F′ of each half is:
F′=F2
Since the original focal length F=15 cm, the focal length of each half is:
F′=152=30 cm
The focal length of each half of the lens is 30 cm.
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Very short answer question
5 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - very short answer questions
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Focal length of a convex lens in air is 25 cm. It is cut into two equal halves along its principal axis. What will be the focal length of each half ?
View SolutionA equiconcave lens of focal length 15 cm is cut into two equal havles along dotted lines as shown in figure. What will be new focal length of each half.

View Solution
Knowledge Check
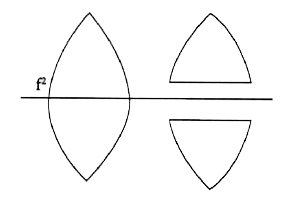
If a symmetrical convex lens of focal length 'f is cut into two parts along the principal axis as shown in the figure, the focal length of each part will be:
 Af2Bf4CfD∞
Af2Bf4CfD∞The figure shows and equiconvex lens of focal length f. It the lens is cut along PQ, the focal length of each half will be
 Af2BfC2fD4f
Af2BfC2fD4fA biconvex lens has a focal length of 10 cm. It is cut in half and two pieces are placed as shown. The focal length of the final combination is
 A10B20C40DNot a lens
A10B20C40DNot a lens
A diverging lens of focal length F is cut into two idential parts, each forming a plano concave lens, Fig. What is the focal length of each part ?

View SolutionIf a convex lens of focal length 20 cm and a concave lens of focal length 30 cm are kept in contract with each other.
What will be the focal length of the combination ?
View SolutionIf the convex lens of focal length 10 cm and a concave lens of focal length 50 cm are kept in contact with each other.
What will be the focal length of the combination ?
View SolutionA thin double convex lens of focal length f is broken into two equal halves at the axis. The two halves are combined as shown in figure. What is the focal length of combination in (ii) and (iii).
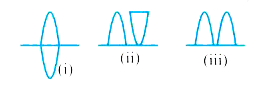
View SolutionAn equiconcave diverging lens of focal length F is cut into two equal halves. The two halves are turned around and joined with some liquid between them.The lens obtained is converging with focal length F. If the refractive index of the liquid is 3 then what is the refractive index of the lens?
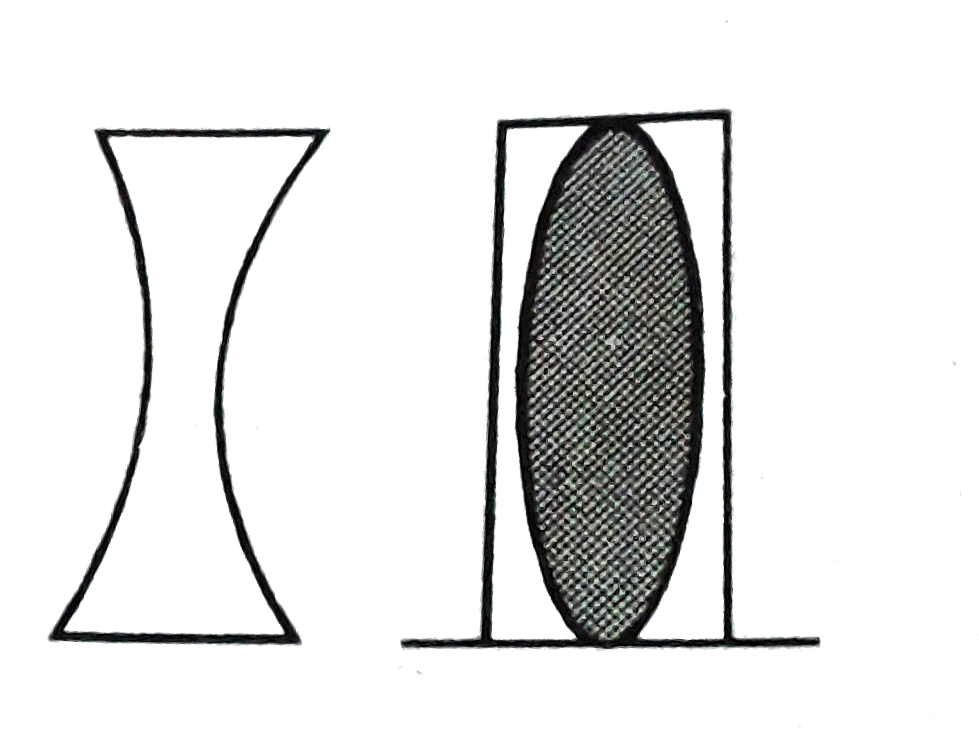
View Solution
