When a fish looks up the surface of a perfectly smooth lake, the surface appears dark except inside a circular area directly above it. Calculate the angle that this illuminated region subtends. Given μ of water =1.333.
The correct Answer is:97.2∘
Here, μ=1.333,2θ=?
sinC=1μ=11.333=0.75
C=sin−1(0.75)=48.6∘.
Angle which illuminated region subtends
=2θ=2C=2×48.6∘=97.2∘
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Problems for practice4videos
OPTICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Comprehension 11videos
OPTICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Value based questions3videos
OPTICS
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
A salt water lake has refractive index 1.4. A fish when looks towards the surface of water, can only view things outside through a circular area. Calculate the semi-vertical angle of the cone formed within which the circular area lies.
View SolutionA point source is placed at a depth h below the surface of water (refractive index = mu). (a) Show that light escapes through a circular area on the water surface with its centre directly above the point source. (b) Find the angle subtended by a radius of the area on the source.
View Solution
Knowledge Check
- Question 1 - Select One
A ball is dropped from a height of 20m above the surface of water in a lake. The refractive index of water is 4/3. A fish inside the lake , in the line fall of the ball, is looking at the ball. At an instant when the balll is 12.8m above the water surface, the fish sees the speed of ball as .
A9ms−1B12ms−1C16ms−1D21.33ms−1 - Question 2 - Select One
A bird in air looks at a fish vertically below it and inside water. h1 is the height of the bird above the surface of water and h2, the depth of the fish below the surface of water. If refractive index of water with respect to air be μ, then the distance of the fish as observed by the bird is
Ah1+h2Bh1+h2μCμh1+h2Dμh1+μh2 - Question 3 - Select One
A ball is dropped from a height of 20 m above the surface of water in a lake. The refractive index of water is 4.3. A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is 12.8 m above the water surface, the fish sees the speed of the ball as [Takeg=10ms2.]
A9 m/sB12 m/sC16 m/sD21.33 m/s
In a river 2m deep a water level measuring post embedded into the river stand vertically with 1 m of if above the water surface.If the angle of inclination of sum above the horizon is 30∘, calculate the length of the post on the bottom surface of river , (μ for water = 4/3 )
3.44 mView SolutionA point source of light is placed directly below the surface of a lake at a distance h from the surface. Find the area surface of a lake at a distance h from the surface. Find the area on water from which the light will come out from water.
[πh2(μ2−1)]View SolutionA plane mirror is fixed at the bottom of a vessel as shown in the figure. Water of refractive index μ is filled up to a height h in the vessel. There is a fish at a height h/2 from bottom of vessel and there is a bird at a height h above the surface of water in the vessel.
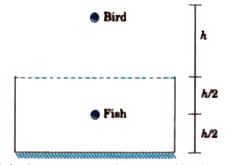
(a) Calculate apparent distance of bird as seen by the fish.
(b) Calculate apparent distance of image of bird in mirror as seen by the fish.
(c) Calculate apparent distance of fish as seen by the bird.
(d) Calculate apparent distance of image of fish in the mirror as seen by the bird.View SolutionA point source of light is placed at a distance h below the surface of a large deep lake.
(a) Show that the fraction f of the light energy that escapes directly from the water surface is independent of h and is given by f=12−12n√n2−1 where n is the index of refraction of water.
(Note: Absorption within the water and reflection at the surface, except where it is total, have been neglected)
(b) Evaluate this ratio for n=4/3.View SolutionA ball is dropped from a height of 20m above the surface of water in a lake. The refractive index of water is 4/3. A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is 12.8m above the water surface, the fish sees the speed of ball as (g=10m/sec2)
View Solution

