For a parallel beam of monochromatic light of wavelength 'λ' differaction is produced by a single slit whose width 'a' is of the order as wavelength of the light. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
Dλ
Daλ
2Daλ
2Dλa
The correct Answer is:D
As angular width, θ=λa
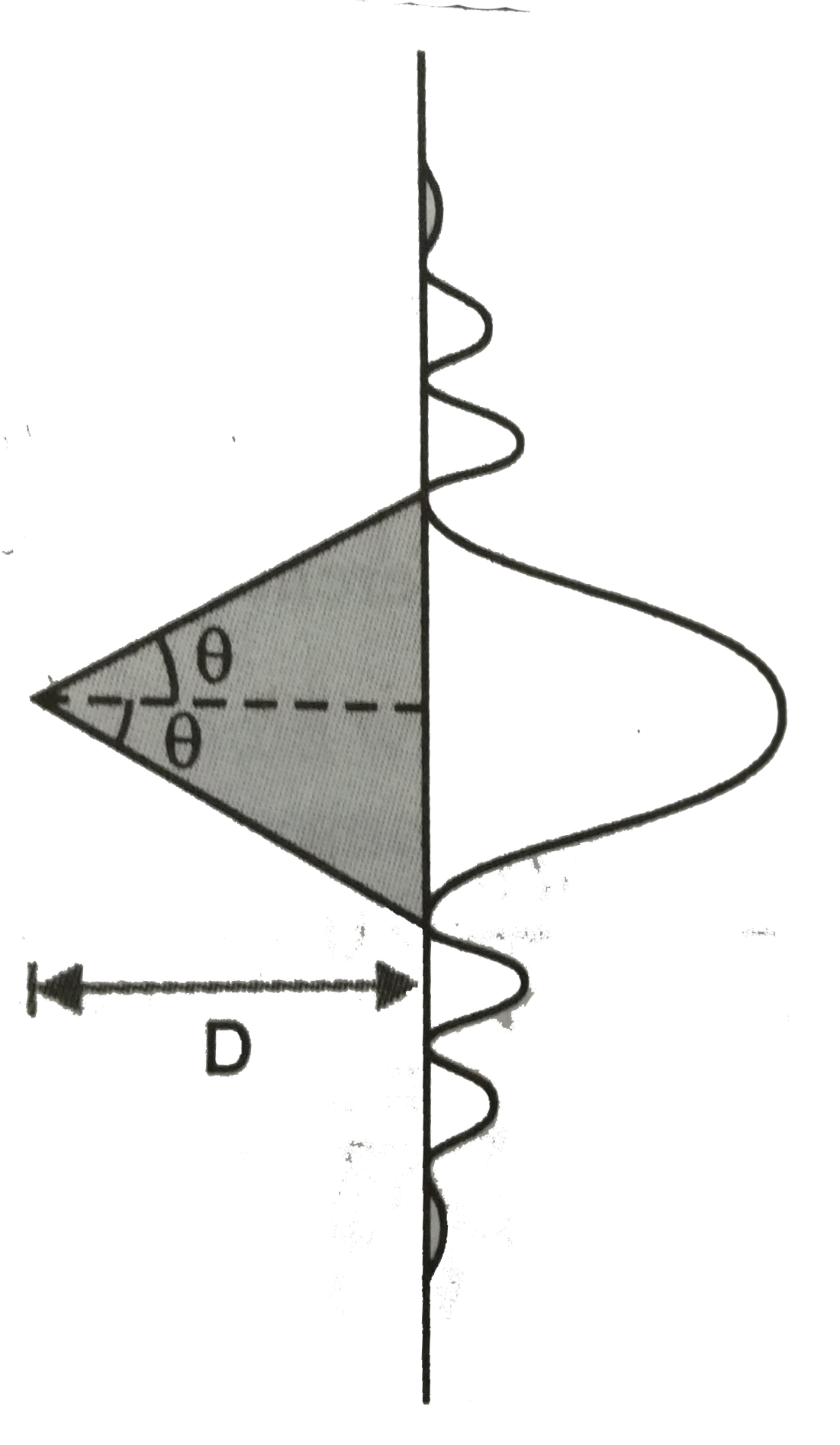
In Fig.
2θ=arcradius≈Linear widthD
∴ Linear width of central maxima =2Dθ
width of central maxima =2Dλa
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Problems for practice
4 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Comprehension 1
1 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Value based questions
3 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
A monochromatic light of wavelength λ falls on a single slit. The first secondary maximum occurs at 30∘ if the width of the slit is equal to
View SolutionA single slit of width 0.20mm is illuminated with light of wavelength 500nm. The observing screen is placed 80cm from the slit. The width of the central bright fringe will be
View Solution
Knowledge Check
For a parallel beam of monochromatic light of wavelength 'λ' diffraction is produced by a single slit whose width 'a' is of the order of the wavelength of the light. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
A(a) 2DλaB(b) DλaC(c) DaλD(d) 2DaλFor a parallel beam of monochromatic. Light of wavelength 'λ' diffraction is produced by a single slit whose width 'a' is of the order of the wavelength of the lightl. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
A2DλaBDλaCDaλD2DaλFor a parallel beam of monochromatic light of wavelength 'λ' diffraction is produced by a single slit whose width 'a' is of the order of the wavelength of the light. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
ADλaBDa/λC12D/aD2Dλa
A single slit of width 0.20mm is illuminated with light of wavelength 500nm. The observing screen is placed 80cm from the slit. The width of the central bright fringe will be
View SolutionA single slit of width 0.20mm is illuminated with light of wavelength 500nm. The observing screen is placed 80cm from the slit. The width of the central bright fringe will be
View SolutionLight of wavelength 6328Å is incident normally on a slit having a width of 0.2mm. The distance of the screen from the slit is 0.9m. The angular width of the central maximum is
View SolutionA parallel beam of light of wavelength 6000Å gets diffracted by a single slit of width 0.3 mm. The angular position of the first minima of diffracted light is :
View SolutionMonochromatic light of wavelength 580 nm is incident on a slit of width 0.30 mm. The screen is 2m from the slit . The width of the central maximum is
View Solution
