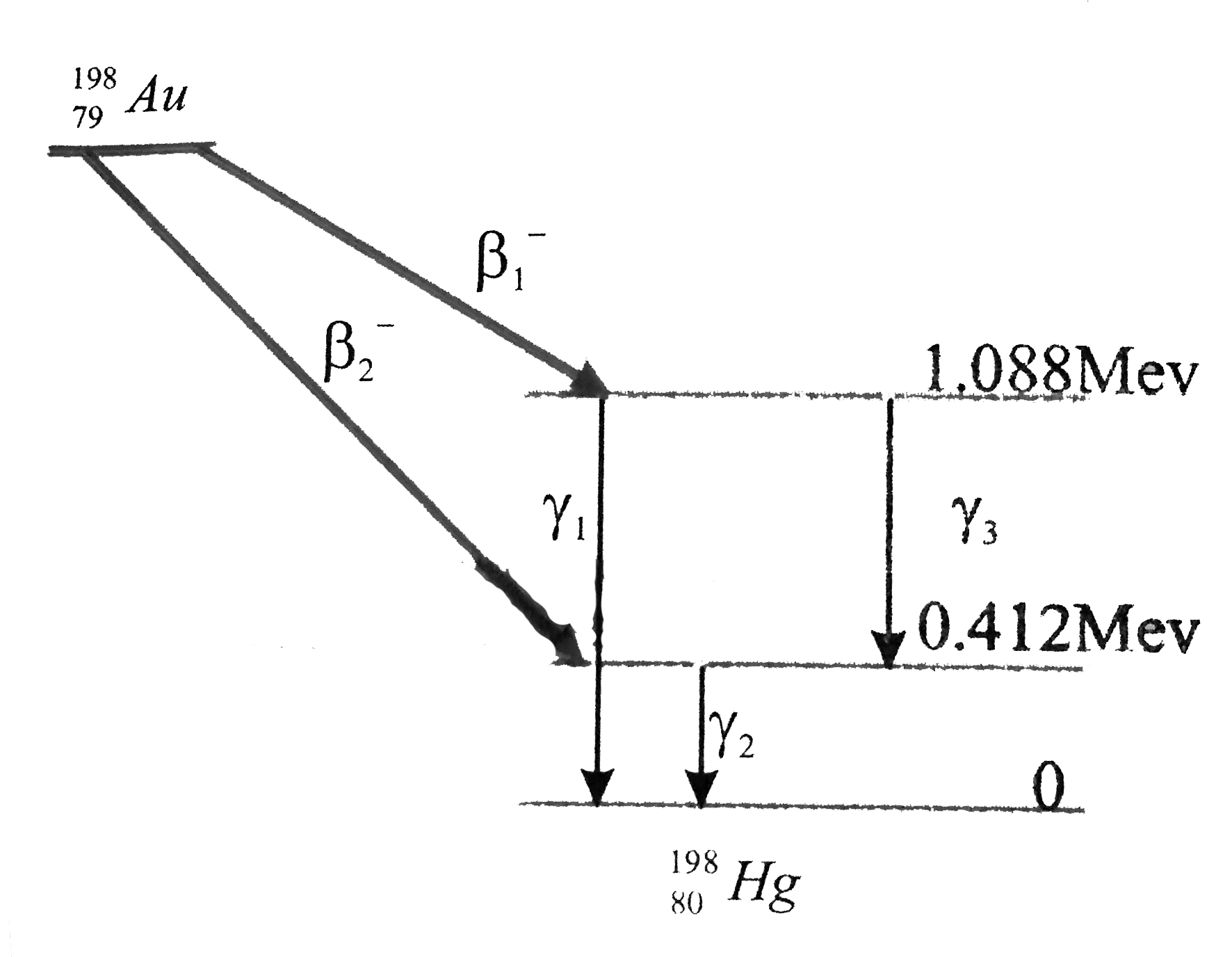
Consider the beta decay
$^198 A u \to^{198} H g * + B η^{- 1} + \to v$ .
where $^198 H g^{*}$ represents a mercury nucleus in an excited state at energy $1.088 M e V$ above the ground state. What can be the maximum kinetic energy of the electron emitted? The atomic mass of $^198 A u$ is $197.968233 u$ and that of $^198 H g$ is $197.966760 u$ .

Video Solution

Text Solution

Verified by Experts

Mass defect in the process
$Δ m = 197.968233 - 197.966760$
$= 0.001473 a . m . u .$
$∴$ Total B.E. $= 0.001473 \times 931 M e V$
$= 1.3786 M e V .$
As Hg is in excited state with an energy of 1.088MeV, therefore, max. possible K.E. of electron emitted is $= 1.3786 - 1.088 = 0.2806 M e V$

|

Updated on:21/07/2023

Class 12 PHYSICS ATOMIC PHYSICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
During $β$ -decay of stationary nucleus , an electron is observed with a kinetic energy 1.0 MeV . From this ,what can be concluded about the Q-value of the decay ?
AQ=1.0 MeV
B $Q \leq 1.0 M e V$
C $Q \geq 1.0 M e V$
DNoting can be concluded about the Q-value
Question 2 - Select One
Gold $._{79}^{198} A u$ undergoes $β^{-}$ decay to an excited state of $._{80}^{198} H g$ . If the excited state decays by emission of a $γ$ -photon with energy $0.412 M e V$ , the maximum kinetic energy of the electron emitted in the decay is (This maximum occurs when the antineutrino has negligible energy. The recoil energy of the $._{80}^{198} H g$ nucleus can be ignored. The masses of the neutral atoms in their ground states are $197.968255 u$ for $._{79}^{198} H g$ ).
A $0.412 M e V$
B $1.371 M e V$
C $0.959 M e V$
D $1.473 M e V$

PRADEEP-ATOMS AND NUCLEI-Assertion- Reason type question 12

Home
Ask Doubt
Profile