A free proton cannot decay into (n+e++v), because such decay is not energetically allowed. Yet we observe in nature beta decay with positron emission. How do we understand the emission of positrons form nuclei?
To understand why a free proton cannot decay into a neutron, a positron, and a neutrino, while we do observe positron emission from certain nuclei (beta plus decay), we can break down the explanation into several steps:
1. Understanding Free Proton Decay:
- A free proton (p) cannot decay into a neutron (n), a positron (e+), and a neutrino (ν) because this reaction is not energetically favorable. The mass-energy of the products (n + e+ + ν) is greater than that of the initial proton.
2. Energy Considerations:
- The decay process can be analyzed using the concept of Q-value, which is defined as the difference in mass-energy between the initial and final states. For the decay of a free proton:
Q=(mp−(mn+me++mν))c2
- Since the mass of the neutron is greater than that of the proton, the Q-value becomes negative, indicating that energy must be supplied for the decay to occur, which is not possible in free space.
3. Nuclear Binding Energy:
- In contrast, within a nucleus, protons and neutrons are bound together by the strong nuclear force. The binding energy of the nucleus plays a crucial role in making certain decay processes energetically favorable.
4. Beta Plus Decay:
- In beta plus decay (β+ decay), a proton in a nucleus can transform into a neutron while emitting a positron and a neutrino. This process is energetically allowed because the mass-energy of the parent nucleus (which includes the binding energy) is greater than that of the daughter nucleus.
- The reaction can be represented as:
p→n+e++ν
- Here, the binding energy of the daughter nucleus (which contains one less proton and one more neutron) is higher than that of the parent nucleus, making the decay energetically favorable.
5. Conclusion:
- Therefore, while a free proton cannot decay into a neutron and positron due to unfavorable energy conditions, the presence of binding energy in a nucleus allows for the emission of positrons during beta plus decay.
- A free proton (p) cannot decay into a neutron (n), a positron (e+), and a neutrino (ν) because this reaction is not energetically favorable. The mass-energy of the products (n + e+ + ν) is greater than that of the initial proton.
- The decay process can be analyzed using the concept of Q-value, which is defined as the difference in mass-energy between the initial and final states. For the decay of a free proton:
Q=(mp−(mn+me++mν))c2
- Since the mass of the neutron is greater than that of the proton, the Q-value becomes negative, indicating that energy must be supplied for the decay to occur, which is not possible in free space.
- In contrast, within a nucleus, protons and neutrons are bound together by the strong nuclear force. The binding energy of the nucleus plays a crucial role in making certain decay processes energetically favorable.
- In beta plus decay (β+ decay), a proton in a nucleus can transform into a neutron while emitting a positron and a neutrino. This process is energetically allowed because the mass-energy of the parent nucleus (which includes the binding energy) is greater than that of the daughter nucleus.
- The reaction can be represented as:
p→n+e++ν
- Here, the binding energy of the daughter nucleus (which contains one less proton and one more neutron) is higher than that of the parent nucleus, making the decay energetically favorable.
- Therefore, while a free proton cannot decay into a neutron and positron due to unfavorable energy conditions, the presence of binding energy in a nucleus allows for the emission of positrons during beta plus decay.
Topper's Solved these Questions
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - (I) Conceptual Problems 18
1 Video
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - (I) Conceptual Problems 21
1 Video
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - (I) Conceptual Problems 14
1 Video
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
Similar Questions
The emission of an αoraβ particle by a radioactive element forms a new element. However, successive emission of some αorβ- particles may give rise to an isotope or an isobar of the original element. In many cases, positron emission or K− electron capture takes place, leading again to the formuation of new elements, alongwith the emission of neutrinos or antineutrinos. These emission also change the neutron/proton (n/p) ratio so that they give rise to stable isotopes which lie in the stability belt. However, in any disintegration reaction, the law of conservation of atomic number and mass number is always obeyed and this helps us to calculate the number of αandβ− particles emitted in the reaction.
Positron emission result in
View SolutionThe β-decay process, discovered around 1900, is basically the decay of a neutron (n), In the laboratory, a proton (p) and an electron (e−) are observed as the decay products of the neutron. Therefore, considering the decay of a neutron as a tro-body dcay process, it was observed that the electron kinetic energy has a continuous spectrum. Considering a three-body decay process i.e., n→p+e−+−ve, around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino (−Ve) to be massless and possessing negligible energy, and neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is 0.8×106eV. The kinetic energy carried by the proton is only the recoil energy.
What is the maximum energy of the anti-neutrino?
View Solution
Knowledge Check
.21483Bi decays to A by α -emission . A then decays to B by beta emission , which further decays to C by another beta emission . Element C decays to D by still another beta emission , and D deacays by α-emission to form a stable isotope E. What is element E?
A_(81)207T1B_(80)206HgC_(79)206AuD_(82)206PbDuring alpha-decay , a nucleus decays by emitting an α-particle ( a helium nucleus .2He4) according to the equation
.AZX→.A−4Z−2Y+.42He+Q
In this process, the energy released Q is shared by the emitted α-particle and daughter nucleus in the form of kinetic energy .
The energy Q is divided in a definite ratio among the α-particle and the daughter nucleus .
A nucleus that decays spontaneously by emitting an electron or a positron is said to undergo β-decay .This process also involves a release of definite energy . Initially, the β-decay was represented as .AZX→.AZ+1Y+e−(electron)+Q
According to this reaction, the energy released during each decay must be divided in definite ratio by the emitted e' (β-particle) and the daughter nucleus. While , in alpha decay, it has been found that every emitted α-particle has the same sharply defined kinetic energy. It is not so in case of β-decay . The energy of emitted electrons or positrons is found to vary between zero to a certain maximum value. Wolfgang Pauli first suggested the existence of neutrinoes in 1930. He suggested that during β-decay, a third particle is also emitted. It shares energy with the emitted β particles and thus accounts for the energy distribution.
During β+ decay (positron emission) a proton in the nucleus is converted into a neutron, positron and neutrino. The reaction is correctly represented asA.AZX→.A−1Z−1X+e++v+ EnergyB.AZX→. AZ−1X+e++v+ EnergyC.AZX→.AZ−1X+e++v+ EnergyD.AZX→.A−1ZX+e++v+ EnergyDuring alpha-decay , a nucleus decays by emitting an α-particle ( a helium nucleus .2He4) according to the equation
.AZX→.A−4Z−2Y+.42He+Q
In this process, the energy released Q is shared by the emitted α-particle and daughter nucleus in the form of kinetic energy .
The energy Q is divided in a definite ratio among the α-particle and the daughter nucleus .
A nucleus that decays spontaneously by emitting an electron or a positron is said to undergo β-decay .This process also involves a release of definite energy . Initially, the β-decay was represented as .AZX→.AZ+1Y+e−(electron)+Q
According to this reaction, the energy released during each decay must be divided in definite ratio by the emitted e' (β-particle) and the daughter nucleus. While , in alpha decay, it has been found that every emitted α-particle has the same sharply defined kinetic energy. It is not so in case of β-decay . The energy of emitted electrons or positrons is found to vary between zero to a certain maximum value. Wolfgang Pauli first suggested the existence of neutrinoes in 1930. He suggested that during β-decay, a third particle is also emitted. It shares energy with the emitted β particles and thus accounts for the energy distribution.
The beta particles (positron) are emitted with different kinetic energies becauseANeutrino shares a definite amount of energy with positronBThe disintegration energy is shared between positron and neutrino in varying proportionsCNeutrino is massless and carries no energyDNeutrino possesses very high kinetic energy
Various rules of thumb have seen proposed by the scientific community to expalin the mode of radioactive decay by various radioisotopes. One of the major rules is called the n/p ratio. If all the known isotopes of the elemnts are plotted on a graph of number of neutrons (n) versus number of protons (p), it is observed that all isotopes lying outside of a ''stable'' n/p ratio region are radioactive as shown fig. The graph exhibits straight line behaviour with unit slope up to p=25. Above p=25, tgose isotopes with n/p ratios lying above the stable region usually undergo beta decay. Very heavy isotopes (p>83) are unstable because of their relativley large nuclei and they undergo alpha decay. Gamma ray emission does not involve the release of a particle. It represnts a change in an atom from a higher energy level to a lower energy level.
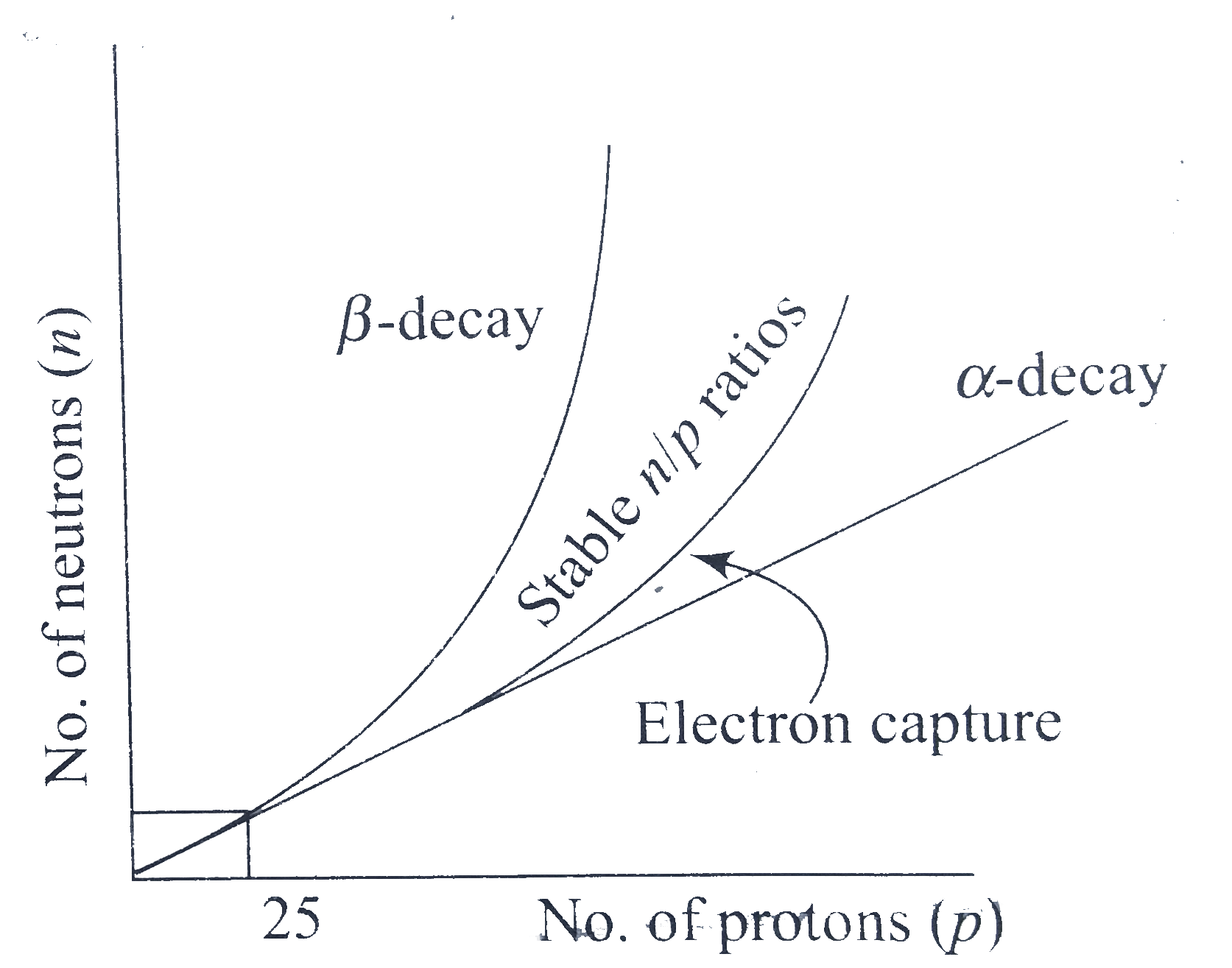
How would the radioisotope of magnesium with atomic mass 27 undergo radioactive decay?.
View SolutionDuring alpha-decay , a nucleus decays by emitting an α-particle ( a helium nucleus .2He4) according to the equation
.AZX→.A−4Z−2Y+.42He+Q
In this process, the energy released Q is shared by the emitted α-particle and daughter nucleus in the form of kinetic energy .
The energy Q is divided in a definite ratio among the α-particle and the daughter nucleus .
A nucleus that decays spontaneously by emitting an electron or a positron is said to undergo β-decay .This process also involves a release of definite energy . Initially, the β-decay was represented as .AZX→.AZ+1Y+e−(electron)+Q
According to this reaction, the energy released during each decay must be divided in definite ratio by the emitted e' (β-particle) and the daughter nucleus. While , in alpha decay, it has been found that every emitted α-particle has the same sharply defined kinetic energy. It is not so in case of β-decay . The energy of emitted electrons or positrons is found to vary between zero to a certain maximum value. Wolfgang Pauli first suggested the existence of neutrinoes in 1930. He suggested that during β-decay, a third particle is also emitted. It shares energy with the emitted β particles and thus accounts for the energy distribution.
When a nucleus of mass number A at rest decays emitting an α-particle , the daugther nucleus recoils with energy K . What is the Q value of the reaction ?
View SolutionThe emission of an αoraβ particle by a radioactive element forms a new element. However, successive emission of some αorβ- particles may give rise to an isotope or an isobar of the original element. In many cases, positron emission or K− electron capture takes place, leading again to the formuation of new elements, alongwith the emission of neutrinos or antineutrinos. These emission also change the neutron/proton (n/p) ratio so that they give rise to stable isotopes which lie in the stability belt. However, in any disintegration reaction, the law of conservation of atomic number and mass number is always obeyed and this helps us to calculate the number of αandβ− particles emitted in the reaction.
A radioactive element X emits 3α,1βand1γ−particles and forms .76Y235. Element X is
View SolutionThe β-decay process, discovered around 1900, is basically the decay of a neutron (n), In the laboratory, a proton (p) and an electron (e−) are observed as the decay products of the neutron. Therefore, considering the decay of a neutron as a tro-body dcay process, it was observed that the electron kinetic energy has a continuous spectrum. Considering a three-body decay process i.e., n→p+e−+−ve, around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino (−Ve) to be massless and possessing negligible energy, and neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is 0.8×106eV. The kinetic energy carried by the proton is only the recoil energy.
If the anti-neutrino has a mass of 3eV/c2 (where c is the speed of light) instead of zero mass, what should be the range of the kinetic energy, K of the electron?
View SolutionThe emission of an αoraβ particle by a radioactive element forms a new element. However, successive emission of some αorβ- particles may give rise to an isotope or an isobar of the original element. In many cases, positron emission or K− electron capture takes place, leading again to the formuation of new elements, alongwith the emission of neutrinos or antineutrinos. These emission also change the neutron/proton (n/p) ratio so that they give rise to stable isotopes which lie in the stability belt. However, in any disintegration reaction, the law of conservation of atomic number and mass number is always obeyed and this helps us to calculate the number of αandβ− particles emitted in the reaction.
The number of α−andβ− particle emitted in nuclear reaction .90Th288→.83Bi212 are respectively
View Solution