The Bohr model for the H-atom relies on the Coulomb's law of electrostatics . Coulomb's law has not directly been varified for very short distances of the order of angstroms. Suppos-ing Coulomb's law between two oppsite charge $+ q_{1}, - q_{2}$ is modified to $∣ ∣ \to F ∣ ∣ = \frac{q_{1} q_{2}}{(4 π ε_{0}) r^{2}} \frac{1}{r^{2}}, r \geq R_{0}$
$= \frac{q_{1} q_{2}}{(4 π ε_{0}) r^{2}} \frac{1}{R_{0}^{2}} {(\frac{R_{0}}{r})}^{ε}, r \leq R_{0}$
Calculate in such a case , the ground state enenergy of H-atom , if $ε = 0.1, R_{0} = 1 Å$

Video Solution

Text Solution

Verified by Experts

We are given $∣ ∣ \to F ∣ ∣ = \frac{q_{1} q_{2}}{(4 π ε_{0})} \frac{1}{r^{2}}, r \geq R_{0} ∣ ∣ \to E ∣ ∣ = \frac{q_{1} q_{2}}{(4 π ε_{0})} \frac{1}{R_{0}^{2}} {(\frac{R_{0}}{r^{ε}})}^{ε}, r \leq R_{0}$
$\in = 0.1, R_{0} = 1 Å$ .
Let $\in = 2 + δ$ .
$∴ F = \frac{q_{1} q_{2}}{(4 π ε_{0})} \frac{R_{0}^{δ}}{r^{2 + δ}} = \land \frac{R_{0}^{δ}}{r^{2 + δ}}$ for $r \leq R_{0}$
Where $\land = \frac{q_{1} q_{2}}{4 π ε_{0}} = 9 \times 10^{9} {(1.6 \times 10^{- 19})}^{2} = 23.04 \times 10^{- 29}$
So, $F = \frac{m v^{2}}{r} = \land \frac{R_{0}^{δ}}{r^{2 + δ}} or v^{2} = \frac{\land R_{0}^{δ}}{m r^{1 + δ}} ... ... . (i)$
(i) As $m v r = n h, r = \frac{n h}{m v}$ Using (i), $r = \frac{n h}{m} ⎡ ⎢ ⎣ \frac{m}{{(\land (R_{0}^{δ})]}^{1 / 2}} r^{\frac{1}{2} + \frac{δ}{2}}$
Solving this for r, we get $r_{n} = {[\frac{n^{2} h^{2}}{m \land R_{0}^{δ}}]}^{\frac{1}{1 - δ}}$
for $n = 1, r_{1} = {[\frac{n^{2} h^{2}}{m \land R_{0}^{δ}}]}^{\frac{1}{1 - δ}} = {[\frac{{1.05}^{2} \times 10^{- 68}}{(9.1 \times 10^{- 31}) (23.04 \times 10^{- 29}) 10^{19}}]}^{\frac{1}{2.9}} = 8 \times 10^{- 11} m = 0.08 n m < 0.1 n m$
(ii) form $v_{n} = \frac{n h}{m r_{n}} = n h {(\frac{\land R_{0}^{δ}}{n^{2} h^{2}})}^{\frac{1}{1 - δ}}$ for $n = 1, v_{1} = \frac{h}{m r_{1}} = 1.44 \times 10^{6} m / s$
(iii) $K . E . = \frac{1}{2} m v_{1}^{2} = 9.43 \times 10^{- 19} J = 5.9 e V$ P.E. $(t i l l R_{0}) = - \frac{\land}{R_{0}}$
P.E. form $R_{0}$ to $r = \land R_{0}^{δ} \int_{R_{0}}^{r} \frac{d r}{r^{2 + δ}} = \frac{\land R_{0}^{δ}}{- 1 - δ} {[\frac{1}{r^{1 + δ}}]}_{R_{0}}^{r} = - \frac{\land R_{0}^{δ}}{1 + δ} [\frac{1}{r^{1 + δ}} - \frac{1}{R_{0}^{1 + δ}}] = - \frac{\land}{1 + δ} [\frac{R_{0}^{δ}}{r^{1 + δ}} - \frac{1}{R_{0}}]$
P.E. $= - \frac{\land}{1 + δ} [(\frac{R_{0}^{δ}}{r^{1 + δ}} - \frac{1}{R_{0}} + \frac{1 + δ}{R_{0}}] = \frac{- \land}{- 0.9} [\frac{R_{0}^{- 1.9}}{r^{- 0.9}} - \frac{1.9}{R_{0}}] = \frac{2.3 \times 10^{- 28}}{0.9} [{(0.8)}^{0.9} - 1.9] joule = - 17.3 e V$
$∴$ Total energy = $(- 17.3 + 5.9) e V = - 11.4 e V$

Updated on:21/07/2023

The electrostatic force between two point charges $q_{1}$ and $q_{2}$ at separation r is given by F= $k . \frac{q_{1} q_{2}}{r^{2}}$ . The constant k
ADepends upon system of units only
BDepends upon medium between the charges
CDepends on both 1 and 2
DIs independent of both 1 and 2
A spherical symmetric charge system is centered at origin. Given, Electric potential
$V = \frac{Q}{4 π ε_{0} R_{0}} (r \leq R_{0})$ , $V = \frac{Q}{4 π ε_{0} r} (r > R_{0})$

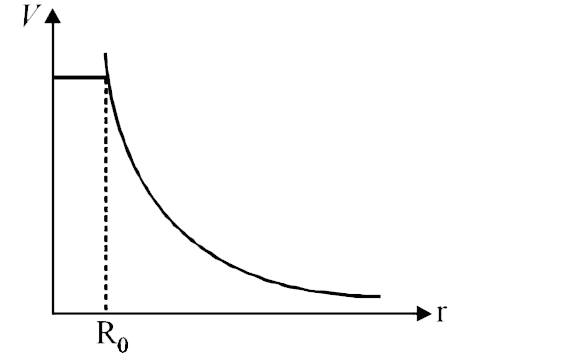A(a) Within $r = 2 R_{0}$ total enclosed net charge is Q
B(b) Electric field is discontinued at $r = R_{0}$
C(c) Charge is only present at $r = R_{0}$
D(d) Electrostatic energy is zero for $r < R_{0}$