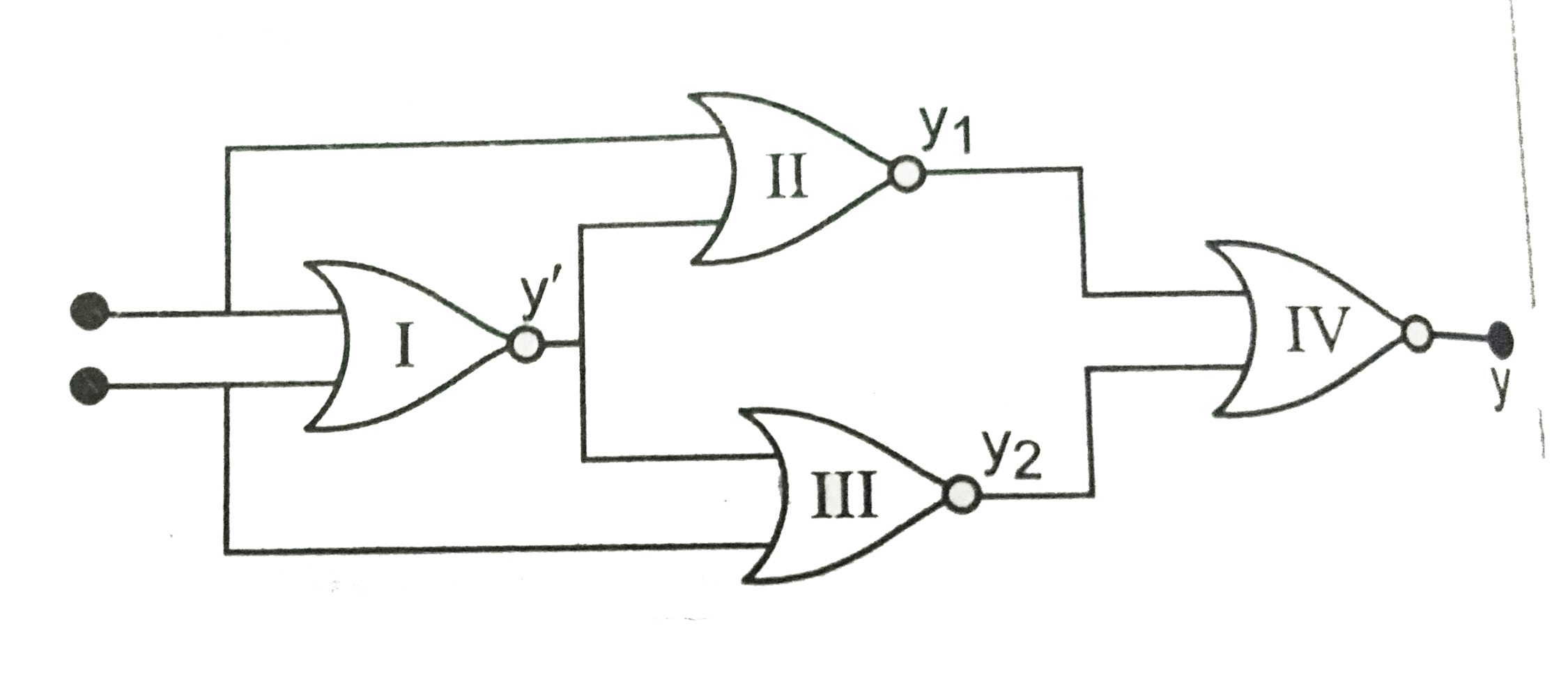
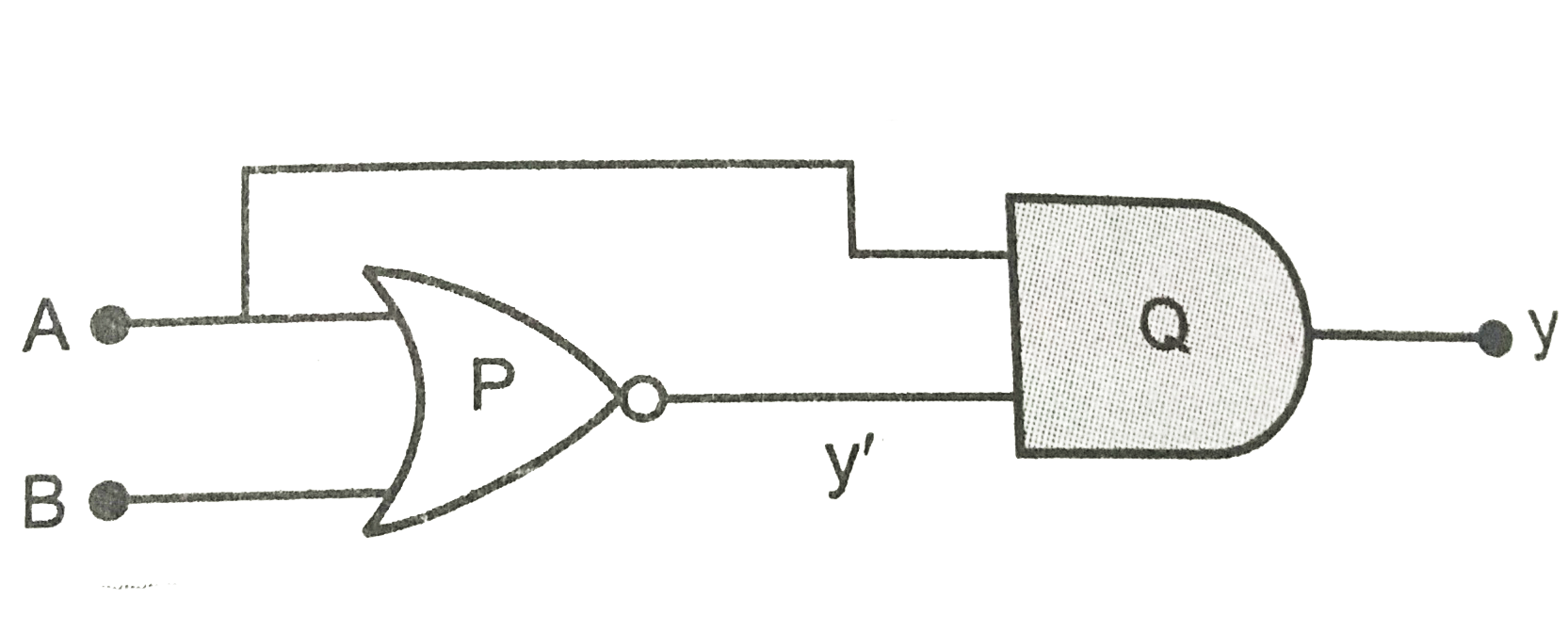
Produce the truth table of the combination of four NAND gates arranged as shown in Fig.Name the gate so formed.
Text Solution
The truth table of combination of gates is shown below,
∣∣
∣
∣
∣
∣
∣∣ABy'(=¯¯¯¯¯¯¯¯A.B)y1(=¯¯¯¯¯¯¯¯¯A.y')y2(=¯¯¯¯¯¯¯B.y)y=¯¯¯¯¯¯¯¯¯y1.y2001110101011011101110110∣∣
∣
∣
∣
∣
∣∣≡∣∣
∣
∣
∣
∣
∣∣ABy000101011110∣∣
∣
∣
∣
∣
∣∣
It means a EXOR gate is produced.
Explaination
Using Boolean expression and De morgan's theorem [i.e., ¯¯¯¯¯¯¯¯C.D=¯¯¯C+¯¯¯Dand¯¯¯¯¯¯¯¯¯¯¯C+D=¯¯¯C.¯¯¯D]
y′=¯¯¯¯¯¯¯¯A.B=¯¯¯A+¯¯¯B
y1=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯A.(¯¯¯A+¯¯¯B)=¯¯¯A+¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(¯¯¯A+¯¯¯B)=¯¯¯A+(¯¯¯¯¯¯¯A.¯¯¯¯¯¯B)=¯¯¯A+(A.B)
y2=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯B.(¯¯¯A+¯¯¯B)=¯¯¯B+¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(¯¯¯A+¯¯¯B)=¯¯¯B+(¯¯¯¯¯¯¯A.¯¯¯¯¯¯B)=¯¯¯B+(A.B)
y=¯¯¯¯¯¯¯¯¯y1.y2=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯[¯¯¯A+(A.B)].[¯¯¯B+(A).B)]=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯[¯¯¯A+(A+B)]=¯¯¯¯¯¯¯A.¯¯¯¯¯¯¯¯¯¯¯A+B+¯¯¯¯¯¯B.¯¯¯¯¯¯¯¯¯¯¯A+B
=A.(¯¯¯A+¯¯¯B)+B.(¯¯¯A+¯¯¯B)=A.¯¯¯A+A.¯¯¯B+B.¯¯¯A+B.¯¯¯B=A.¯¯¯B+B.¯¯¯A(∵A.¯¯¯A=B.¯¯¯B=0)
which is for EXOR gate.
Thus, arrangement works as EXOR gate.
|
Topper's Solved these Questions
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Exercise
312 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - LONG QUESTION ANSWER
2 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - LONG QUESTION ANSWER (NCERT)
4 Videos
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question
5 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS
2 Videos
Similar Questions
Knowledge Check
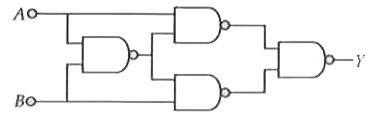
Truth table for system of four NAND gates as shown is
 A
A B
B C
C D
D
The truth table for the following combination of gates is :-
_E01_430_Q01.png) AABY000010101111BABY000010101111CABY001011101110DABY000011101110
AABY000010101111BABY000010101111CABY001011101110DABY000011101110Truth table for system of four NAND gates as shown in figure is :
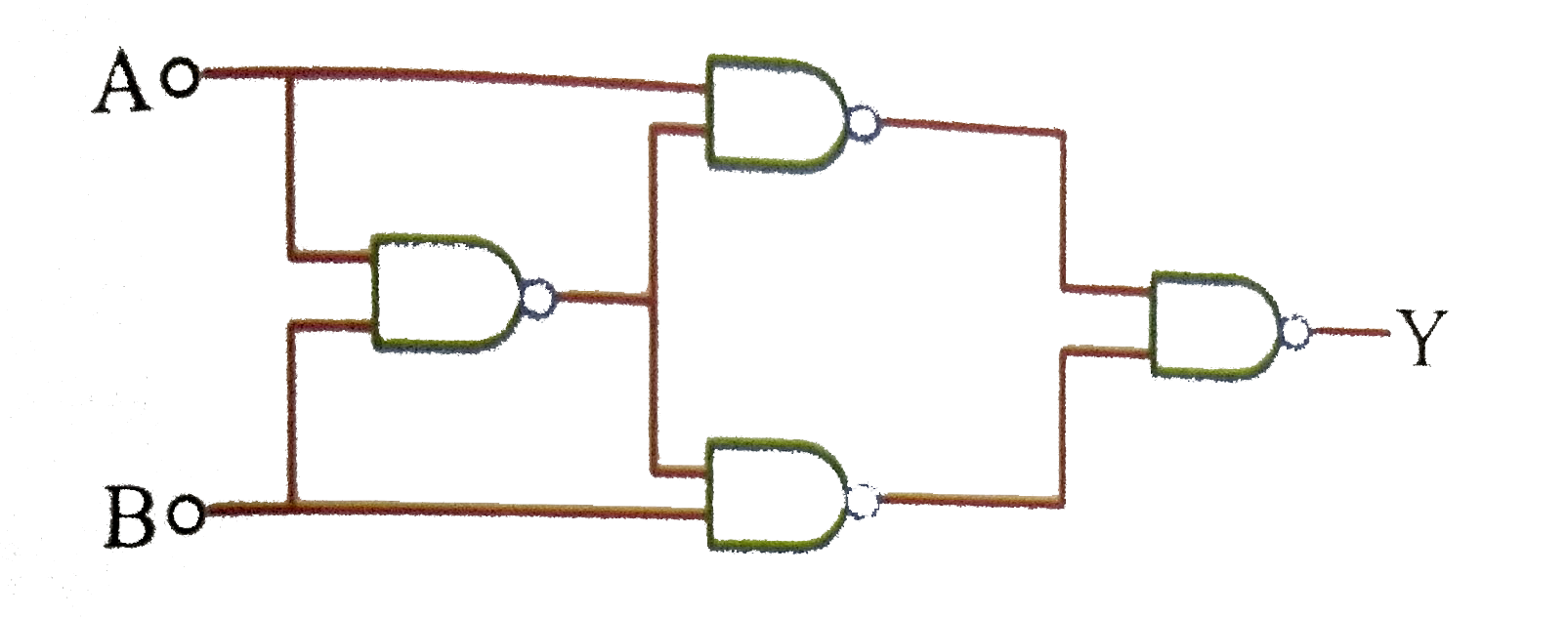 .AABY000011101110BABY000010101111CABY001011100110DABY001010100111
.AABY000011101110BABY000010101111CABY001011100110DABY001010100111
Write the truth table for the combination of the gates shown in the figure.
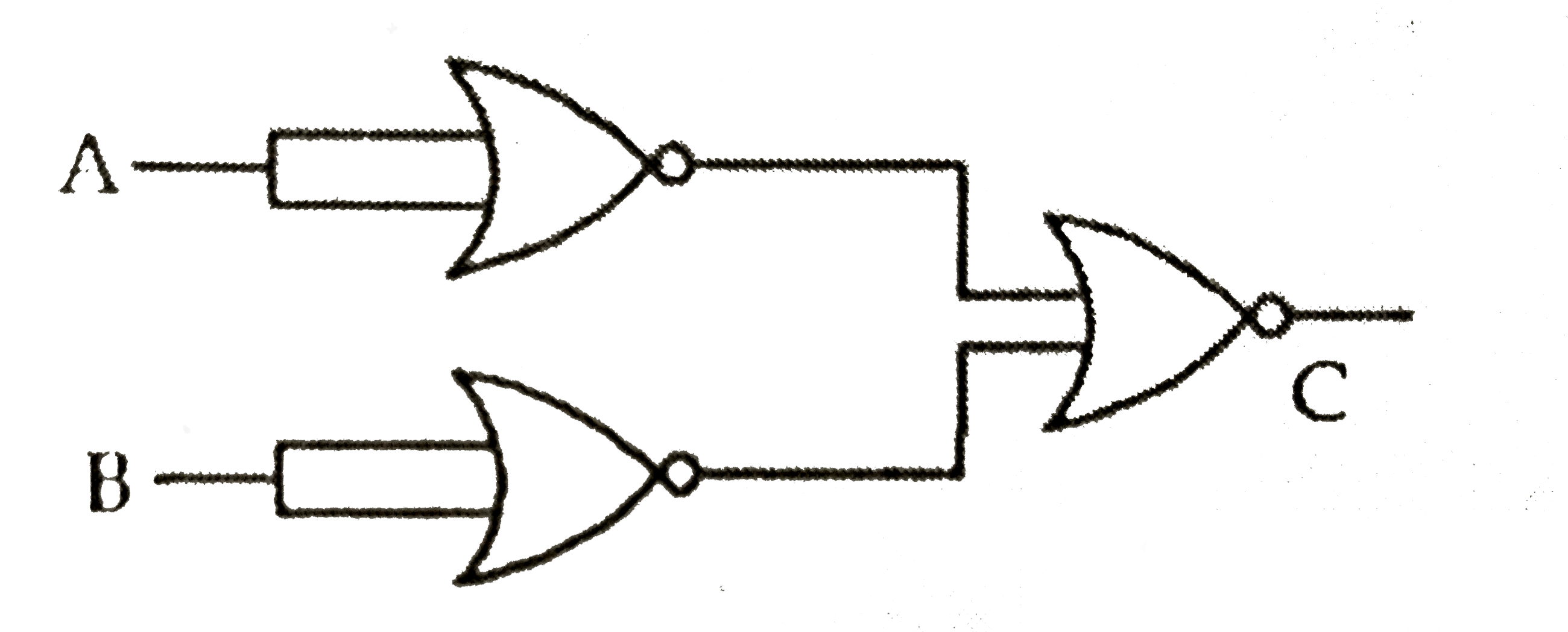
View SolutionGive the truth table and circuit symbol for NAND gate.
View SolutionThe truth table for the following combination of gates is :-
_E01_430_Q01.png)
View SolutionTruth table for system of four NAND gates as shown in figure is
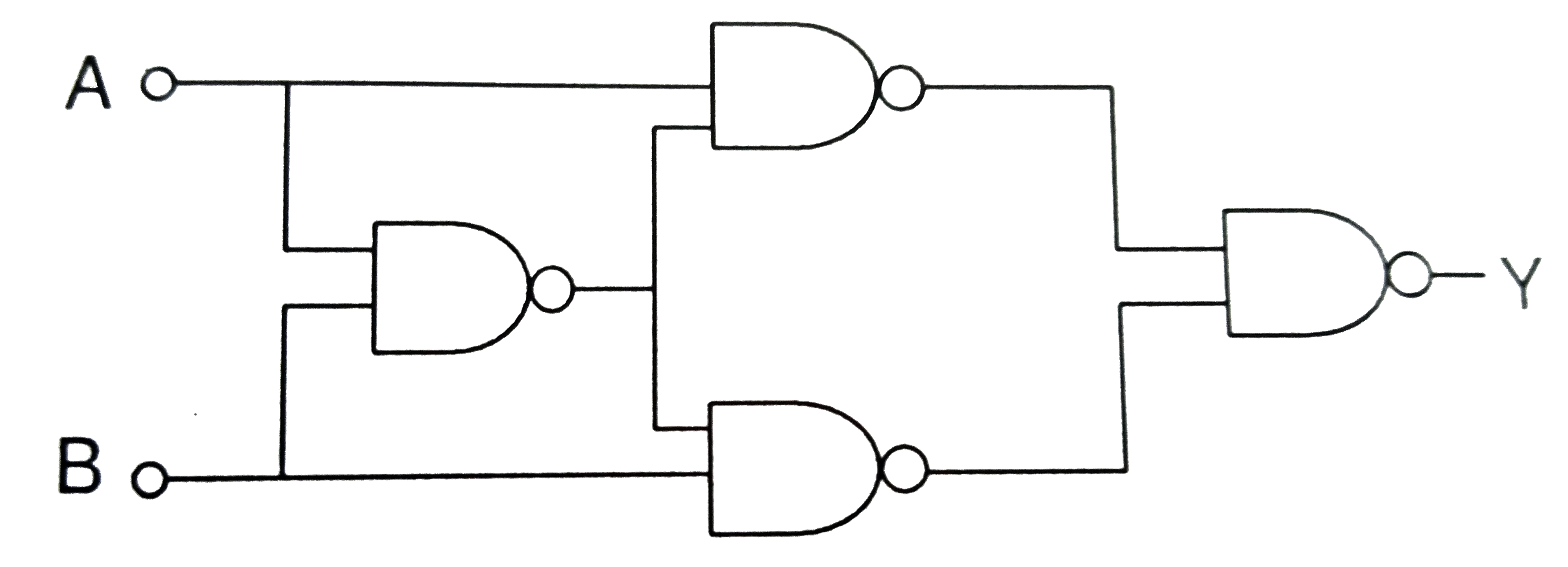
View SolutionTruth table for system of four NAND gates as shown in figure is

View Solution