ABCD is a trapezium in which AB ll CD and AD=BC Show that (i) ∠A=∠B (ii) ∠C=∠D(iii) ΔABC≅ΔBAD (iv) diagonal AC=diagonal BD [Hint Extend AB and draw a line through C parallel to DA intersecting AB produced at E]
Construction
Extent AB to intersect CE||DA at E
InAECD
AB||DC
AE||DC
CE||DA
Both pair of sides are parallel AECD is a parallelogram
AD=CE
AD=BC
BC=CE
In∠BCE
∠ABC≅∠BAD
AC=BD
Similar Questions
Knowledge Check
E is the mid-point of the side AD of the trapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. then
APoint F trisect BCBPoint F bisect BCCAB=CDDNone
In a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC.
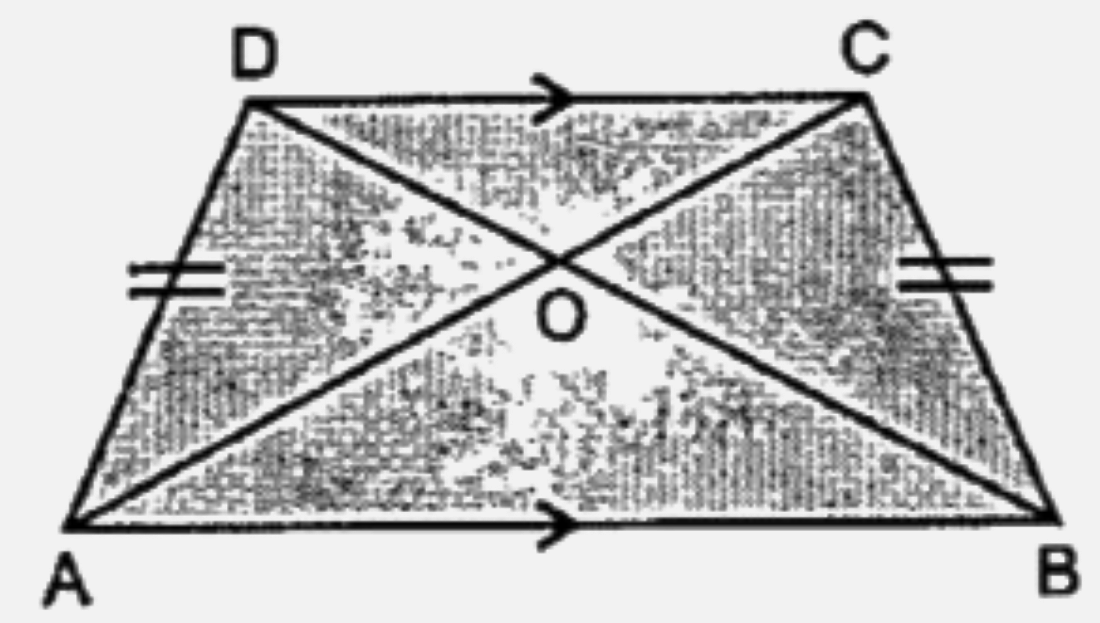
Prove that :
(i) ∠DAB=∠CBA
(ii) ∠ADC=∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD
View SolutionABCD is a rectangle in which diagonal AC bisects ∠Aas well as ∠C. Show that:
(i) ABCD is a square
(ii) diagonal BD bisects ∠Bas well as ∠D..
View SolutionABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C . Show that: (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D. .
View SolutionABCD is a rectangle in which diagonal AC bisects ∠Aas well as ∠C. Show that:(i) ABCD is a square (ii) diagonal BD bisects ∠Bas well as ∠D..
View SolutionLet ABCD be a trapezium ,in which AB is parallel to CD, AB =11 ,BC=4,CD=6 and DA=3. the distance between AB and CD is
View SolutionLet ABCD be a trapezium in which AB is parallel to CD. AB=11,BC=4,CD=6 and DA=3. The distance between AB and CD is
View Solution

