In a circle with centre 'O'PAandPB are two chords. PC is the chord that bisects the angle APB.The tangent to the circle at C is drawn meeting PA and PB extended at Q and R respectively. If QC=3,QA=2andRC=4, then length of RB equals:
In△PQC
(PQ)(AQ)=QC^2
PQ*2=9
PQ=9/2
Sinθ=QCPQ=RCPR
=392=4PR
=PR=6
In△PCR
(PR)(RB)=RC2
6(RB)=16
RB=83
Similar Questions
From an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.
View SolutionFrom an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.
View Solution
Knowledge Check
From a point P outside the circle with centre O, two tangents PA and PB are drawn to meet the circle at A and B respectively. If ∠APB=70∘, then ∠OAB is equal to :
केंद्र O वाले वृत्त के बाहर स्थित किसी बिंदु P से दो स्पर्श रेखाएं PA और PB खींची जाती हैं जो वृत्त से क्रमशः A और B मिलती हैं | यदि ∠APB=70∘ है, तो कोण OAB का मान ज्ञात करें |A35∘B65∘C45∘D55∘If PA and PB are tangents to the circle with centre O such that ∠APB=50∘ then ∠OAB is equal to
A50∘B30∘C40∘D25∘In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
A36∘B18∘C27∘D36∘
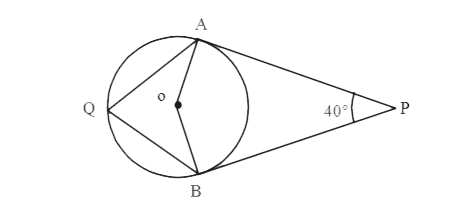
In the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
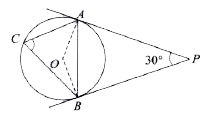
View SolutionIn figure , tangents PA and PB are drawn to a circle such that ∠APB=30∘ and chord AC is drawn parallel to the tangent PB then ∠ABC=
View SolutionFrom a point P two tangents PA and PB are drawn to a circle with centre O.if OP is equal to diameter of the circle then ∠APB is
View SolutionPA and PB are the tangent on a circle with centre O such that ∠APB=42∘. What will be the value of ∠AOB?
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If ∠APB=30∘, then ∠OAB is equal to :
View Solution
